Segment tree
min(1, 2, 3) = 1 And min(3, 2, 1) = 1 will return the same value.In fact, the code doesn't change very much. There are only two important points:
When we prepared the array to build the tree, we filled it with zeros, but this is incorrect in the case of a minimum. Because zeros are very small numbers and they affect the final result. Therefore it is necessary to use a neutral value. That is, a value that does not affect the result. For minimum, for example, you can take this value as INT_MAX. In the code, I moved the neutral value into a separate variable.
int NEUTRAL = INT_MAX;
void resize(vector<int> &arr) {
int s = (int) arr.size();
int new_s = (int) pow(2, ceil(log2(s)));
arr.resize(new_s, NEUTRAL);
}
But what to do with the plus in the segment tree. It's simple: we can change the plus wherever it was used for any associative operation. I changed the plus to a sign ◾which will denote any associative operation.
Building a tree now it looks like this.
void build(vector<int> &arr, int v, int tl, int tr) {
if (tl == tr - 1) {
t[v] = arr[tl];
} else {
int tm = (tl + tr) / 2;
build(arr, v * 2 + 1, tl, tm);
build(arr, v * 2 + 2, tm, tr);
t[v] = t[v * 2 + 1] ◾ t[v * 2 + 2];
}
}
Changing an element
void set(int i, int v, int x, int xl, int xr) {
if (xl == xr - 1) {
t[x] = v;
return;
}
int xm = (xl + xr) / 2;
if (i < xm) {
set(i, v, 2 * x + 1, xl, xm);
} else {
set(i, v, 2 * x + 2, xm, xr);
}
t[x] = t[2 * x + 1] ◾ t[2 * x + 2];
}
Search on a segment
long long sum(int l, int r, int x, int xl, int xr) {
if (r <= xl || l >= xr) {
return NEUTRAL; // обратите внимание, тут тоже нейтральное значение
}
if (xl >= l && xr <= r) {
return t[x];
}
int xm = (xl + xr) / 2;
return sum(l, r, 2 * x + 1, xl, xm) ◾ sum(l, r, 2 * x + 2, xm, xr);
}
Fourth task
Original condition of the problem
Now change the code of the segment tree so that in addition to the minimum on the segment, the number of elements equal to the minimum is also counted
That is
Given an array arr integers of size n. Required m requests. Each request looks like this:
mmin(l,r)– it is necessary to find the minimum, as well as the number of elements equal to the minimum on the segment fromlbeforer - 1set(i, v)– changes the value of an elementarr[i]onv
To solve this problem, we will store a pair of numbers in a tree of segments. The first number is the minimum value itself. And the second is the number of elements on the segment equal to the minimum.
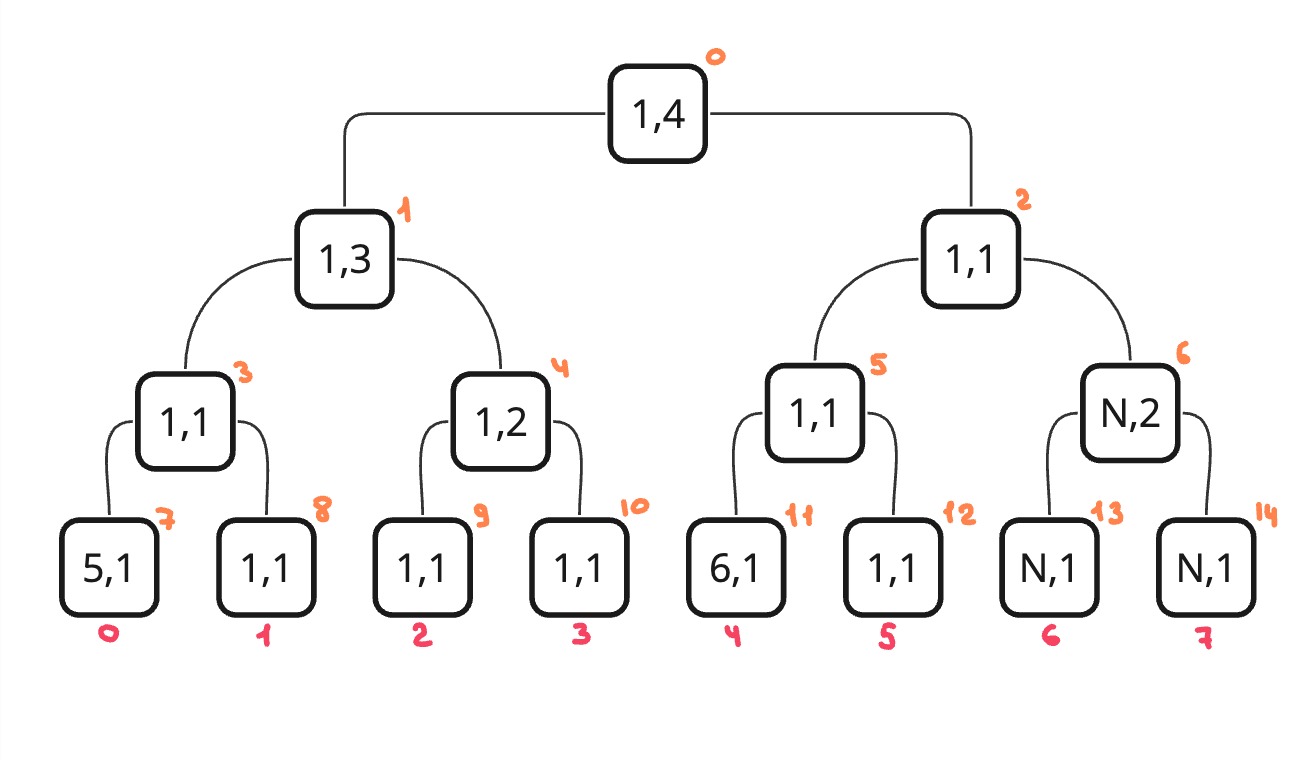
Then we need to define our associative operation. She will accept two pairs. We check if the minimum element of the first pair is less than min. element of the second pair, then we return the first pair. If it’s the other way around, then the second pair. If they are equal, then we need to return a new pair and add the quantities together.
typedef pair<long long, int> Type;
Type combine(Type a, Type b) {
if (a.first < b.first) return a;
if (b.first < a.first) return b;
return {a.first, a.second + b.second};
}
Now we can use this associative operation instead ◾ from the third task. Also don't forget about NEUTRALwhich in this case can be taken as LLONG_MAXand the second value in the pair (NEUTRAL would be a pair) would be 0, since it is a neutral value for addition.
The complete solution can be viewed at GitHub
Fifth task
Original condition of the problem
In this problem you need to add the operation of finding the kth unit to the segment tree
The peculiarity of this problem is that the original array consists only of 1 or 0. And the change operation takes only the index and changes the value to the opposite. That is set(i) -> arr[i] = arr[i] == 1 ? 0 : 1.
To solve this problem, we will store the number of units in the segment in nodes. Then the operation of constructing the tree, as well as the changes, will be the same as in a regular tree of segments. The associative operation will be sum.

But the search for the kth unit will be like this: we will again go down and check the left and right child. If the required k lies in the left child, then we need to go down to the left child. Otherwise you need to go down to the right child. When we descend into the right child, we need to reduce k to the value from the left child.
Let's say we're looking for k = 2, let's start from the root. At the root, our left child is equal to 3 and the right one is also equal 3. This means that in the left segment we have three units, and on the right as well. We need to get the second unit in order. There are three units on the left, which means the second unit will be located exactly there, so we go down to the left. Next, we get a left segment with one unit and a right segment with two units. The left segment is not suitable for us, because we need two units, and there is only one unit on the left, so we go to the right. But here important The right segment does not know anything about how many units were to the left of it, which is why we need to reduce k by the number of units to the left.
int kith(int k, int x, int xl, int xr) {
if (xl == xr - 1) return xl;
int xm = (xl + xr) / 2;
// идем влево, если слева искомое количество единиц
if (t[x * 2 + 1] >= k) {
return kith(k, x * 2 + 1, xl, xm);
} else {
// уменьшаем k, потому что слева уже были какие-то единицы
return kith(k - t[x * 2 + 1], x * 2 + 2, xm, xr);
}
}
The complete solution can be viewed at GitHub
Sixth task
Original problem
In this problem, you need to add to the segment tree the operation of finding, based on data x and l, the minimum index j for which j >= l And a[j] >= x. If there is no such element, then you need to return it -1
In the article e-maxx the general case is indicated when there is also a right border; in their solution, they store in each node a sorted list corresponding to the segment.
In our case, there is no right boundary, so to solve this problem we will use a tree of segments, which is built based on the maximum. That is, each node will store a maximum of children.

The algorithm for finding the minimum index will look like this:
If the current value is less than the desired value
xwe return-1If we went beyond the boundaries
j >= lthen we return-1If we compressed to one element, then we return its index
Otherwise, we check the left and right children one by one and return the result
int above(int v, int l, int x, int lx, int rx) {
if (t[x] < v)
return -1;
if (rx <= l)
return -1;
if (rx == lx + 1) {
return lx;
}
int m = (lx + rx) / 2;
int res = above(v, l, 2 * x + 1, lx, m);
if (res == -1) {
res = above(v, l, 2 * x + 2, m, rx);
}
return res;
}
Let's look at an example when we need to find the minimum index jsuch that j >= 0 And arr[j] >= 3. In the figure below, in purple, I have indicated the result of the function for each node. In doing so, I wrote the calculated values for each node, although in reality the value will only be calculated for nodes with an index (orange number) – 0, 1, 3, 7, 8because before calculating the right one, we calculate the left one and if it is equal -1, then only in this case we calculate the right one. The scheme is this: if there is already some kind of index on the left that is suitable for us, then in principle we no longer need the right side, because it exactly will be greater than the index that was returned on the left.
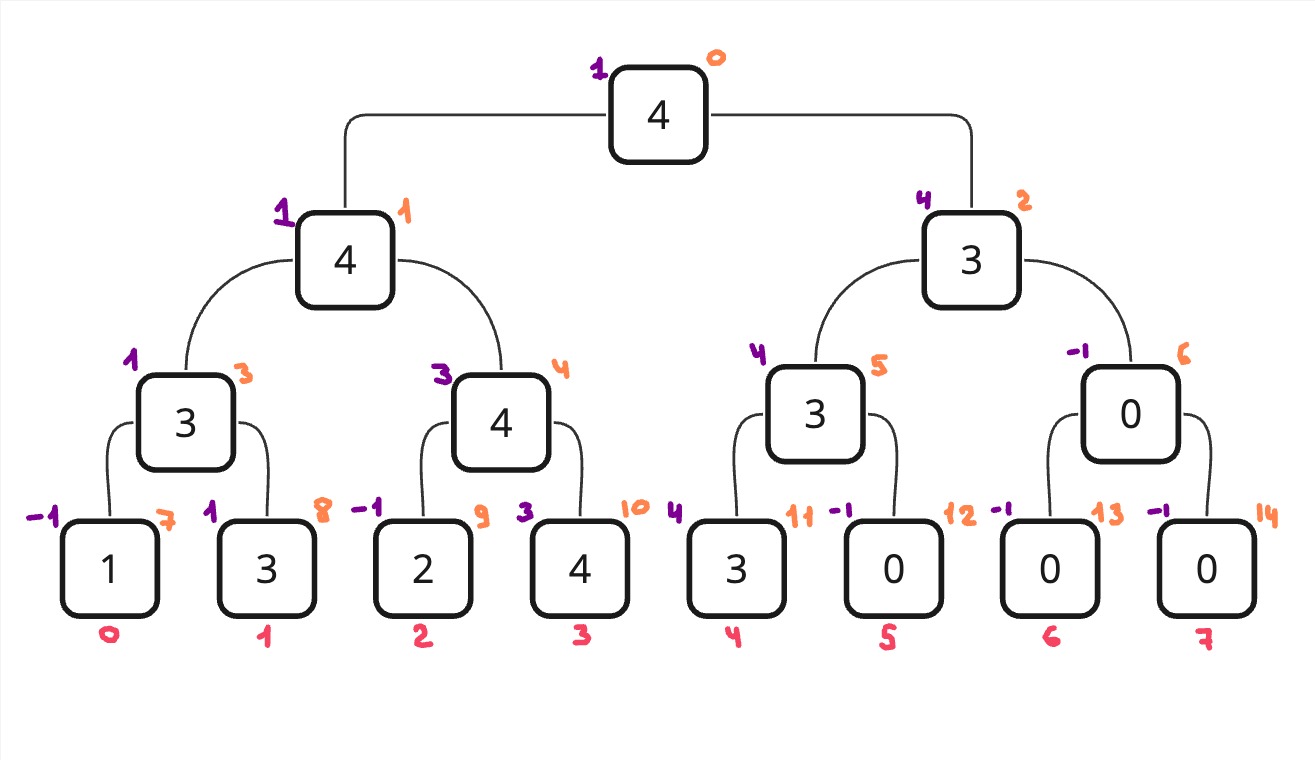
The complete solution can be viewed at GitHub
Fenwick tree
or Binary indexed tree was first described by the Russian mathematician B. Ya. Ryabko in 1989. In 1994, an article by P. Fenwick appeared, where the same structure was described, which was later called Fenwick tree
Let's remember the second problem
Given an array arr integers of size n. Required m requests. Each request looks like this:
sum(l,r)– you need to find the sum of the segment fromlbeforer - 1and return her. Formally:sum(l,r) = a[l] + a[l + 1] + ... + a[r - 1]inc(i, v)– addsvto the value of the elementarr[i]. Essentially, a replacement can be converted into an addition.
Fenwick tree works for O(logn). But there are a number of features
Painting a Fenwick tree is easier
Works a little faster because there are fewer constants
Takes up less memory than a segment tree. The best variant of the segment tree uses
O(2n)memory. The Fenwick tree stores one array of lengthn.
Let's look at the idea in order
Let us have an array f length nwhere each element of the array will be a sum on some segment, that is f[i] = Σ arr[p(i) ... i]. That is, we are conditionally given some iwe are using the function p(i) we obtain the left boundary of the segment and enter it into f[i] sum of elements from the left border (p(i)) to right (i)
How will we calculate the amount from l before r - 1. As we did in the first task, that is, using prefix sums:sum(l, r) = sum(0, r) - sum(0, l)
Let's simplify and do this sum(r) = sum(0, r). How will we calculate sum(r) – that is, the sum of all elements up to r - 1
int sum(int r) {
int i = r - 1;
int res = 0;
while (i >= 0) {
res += f[i];
i = p(i) - 1;
}
return res;
}
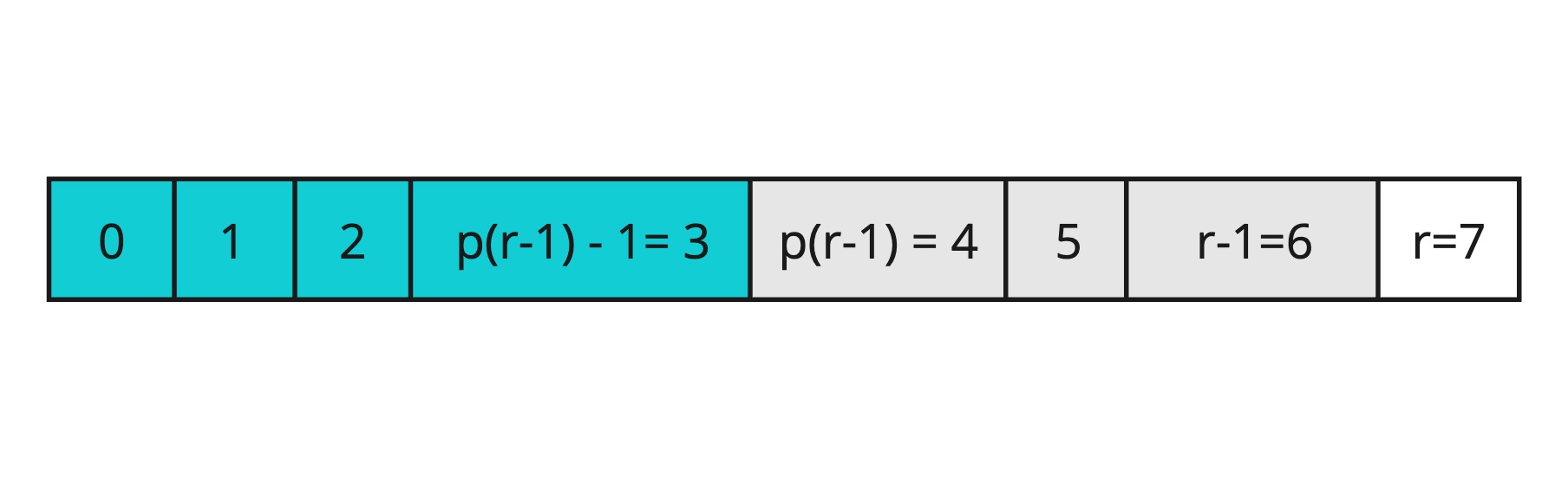
You can see it clearly below. Function p(i) we'll define it later, for clarity, I decided that p(6) = 4
How to execute a function inc(i, v)? To do this you need to find all the indexes of the array f which it falls into i and add value to them v. Let's figure out how to do this quickly later in the text.

How to define a function p(i)?
Let's take the binary representation of a number i – ......011111
And replace all the ones of the last zero with 0 – ......000000
In this case, for every even number p(i) will be equal to this number itself. And for odd numbers, a pattern will form. The function can be defined like this: p(i) = i & (i + 1)
Function sum doesn't change, we just defined the function p(i). A function inc(i, v) now we can determine. We are given i and we need all such indexes jWhat i ∊ [p(j), j]
Let's say we have a binary value j = .....0111 i = .....0???p(j) = .....0000
i lies between j And p(j). Now the opposite is given to us iwe need to find everything j. Essentially, we need to sequentially go through all the zeros in i and change them to one. That is j | (j + 1)
An illustrative example:i = 01010j = 01010 01011 01111 11111
The code looks like this:
void inc(int i, int v) {
int j = i;
while (j < f.size()) {
f[j] += v;
j = j | (j + 1);
}
}
That's it, the Fenwick tree is ready. Unfortunately, the Fenwick tree cannot be used for non-inverse operations, such as for sums we used sum(0,r) - sum(0,l). Full Fenwick tree implementation:
int n;
int a[100000]; //массив
int f[100000]; //дерево Фенвика
int sum(int x) {
int result = 0;
for (; x >= 0; x = (x & (x + 1)) - 1) {
result += f[x];
}
return result;
}
int sum(int l, int r) {
if (l) return sum(r) - sum(l - 1);
else return sum(r);
}
void increase(int idx, int delta) {
a[idx] += delta;
for (; idx < n; idx |= idx + 1) {
f[idx] += delta;
}
}
Seventh task
Condition
Given an array arr integers of size n. Required m requests. Each request looks like this:
max(i)– find the maximum among the elements from0beforeiinc(i, v)– increase the value by indexionvset(i, v)– set value by indexionv. Moreoverv >= arr[i]
This task is called search for maximum on prefix. The Fenwick tree cannot search for a maximum on an arbitrary segment, only on a prefix. The code is very similar to the standard Fenwick tree, the details are slightly different: in this problem f[i] will store a maximum on the segment arr[p(i) ... i]
class fenwick {
public:
explicit fenwick(vector<int> &arr) {
n = (int) arr.size();
a = arr;
f.resize(n, 0);
for (int i = 0; i < arr.size(); ++i) {
set(i, arr[i]);
}
}
int mx(int i) {
int res = INT_MIN;
for (; i >= 0; i = (i & (i + 1)) - 1) {
res = max(res, f[i]);
}
return res;
}
void inc(int i, int v) {
a[i] += v;
for (; i < n; i |= i + 1) {
f[i] += v;
}
}
void set(int i, int v) {
a[i] = v;
for (; i < n; i |= i + 1) {
f[i] = max(f[i], v);
}
}
private:
vector<int> f;
vector<int> a;
int n;
};
Eighth task
Condition
Given an array arr integers of size n. It is necessary to remove the minimum number of elements from it so that the remaining ones form an increasing sequence.
Example: Given an array 6,2,5,4,2,5,6if you remove the indexes 0, 2, 4then we get the sequence 2,4,5,6 – which increases and has the greatest length.
It would seem that this has nothing to do with the tree of segments or the Fenwick tree. But let's slowly figure out how this quickly (for O(nlogn)) decide.
Dynamic programming. O(n^2)
We will store it in an array d meanings, d[i] equal to the length of the largest increasing subsequence that ends in arr[i]
For example, an array d will be equala = 6,2,5,4,2,5,6d = 1,1,2,2,1,3,4
At each iteration we have a choice, either we start a new subsequence, or we join some subsequence on the left. That is d[i] = max(1, max(d[j]) + 1) provided that 0 <= j < i And a[j] < a[i]
Since the subsequence does not necessarily end at the end, the answer will be max(d)
int a[100000];
int d[100000];
int main() {
for (int i = 0; i < n; i++) {
d[i] = 1;
for (int j = 0; j < i; j++) {
if (a[j] < a[i]) {
d[i] = max(d[i], d[j] + 1);
}
}
}
int ans = *max_element(d, d + n);
}
It is easy to see that such a solution will work in O(n^2)
If only it were possible to search for the maximum on the prefix for O(logn). Stop, this is the seventh task, it turns out you can combine dynamic programming and Fenwick tree
class fenwick {
public:
explicit fenwick() {
f.resize(1000001, 0);
}
int mx(int i) {
int res = INT_MIN;
for (; i >= 0; i = (i & (i + 1)) - 1) {
res = max(res, f[i]);
}
return res;
}
void set(int i, int v) {
for (; i < 100000; i |= i + 1) {
f[i] = max(f[i], v);
}
}
private:
vector<int> f;
};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int n;
cin >> n;
vector<int> arr(n);
for (int i = 0; i < n; ++i) cin >> arr[i];
fenwick tree;
for (int i = 0; i < n; ++i) {
int q = tree.mx(arr[i]);
tree.set(arr[i], q + 1);
}
cout << tree.mx(100000);
return 0;
}
If the element is in the original array <= 10^6then you can solve it without problems, otherwise you will need to compress the values.
What means compress value. Let's say we are given an array of length 10^6but the numbers themselves in the array can be from -10^9 before 10^9. That is, in general it matters 10^18 variants of values, which is no longer suitable for the Fenwick tree. Therefore the values need to be compressed. How can I do that. Since we have a limited number of elements, we can define a bijection between the real element and its index. Moreover, two identical elements must return the same index. Thus, even in the worst case, when all numbers are unique, the resulting indices will not exceed 10^6which is suitable for use in Fenwick Wood.
Once again, our index in the Fenwick tree is now value. We can quickly find the maximum in the interval from 0 before i. More clearly (d – this is normal dynamic programming):a = 6,2,5,4,2,5,6d = 1,1,2,2,1,3,4f = 0,0,1,0,2,3,4,0,0....
We iterate through all the elements of the array and do two operations:
Find the maximum value that was before this value
We change the current value to the obtained maximum + 1
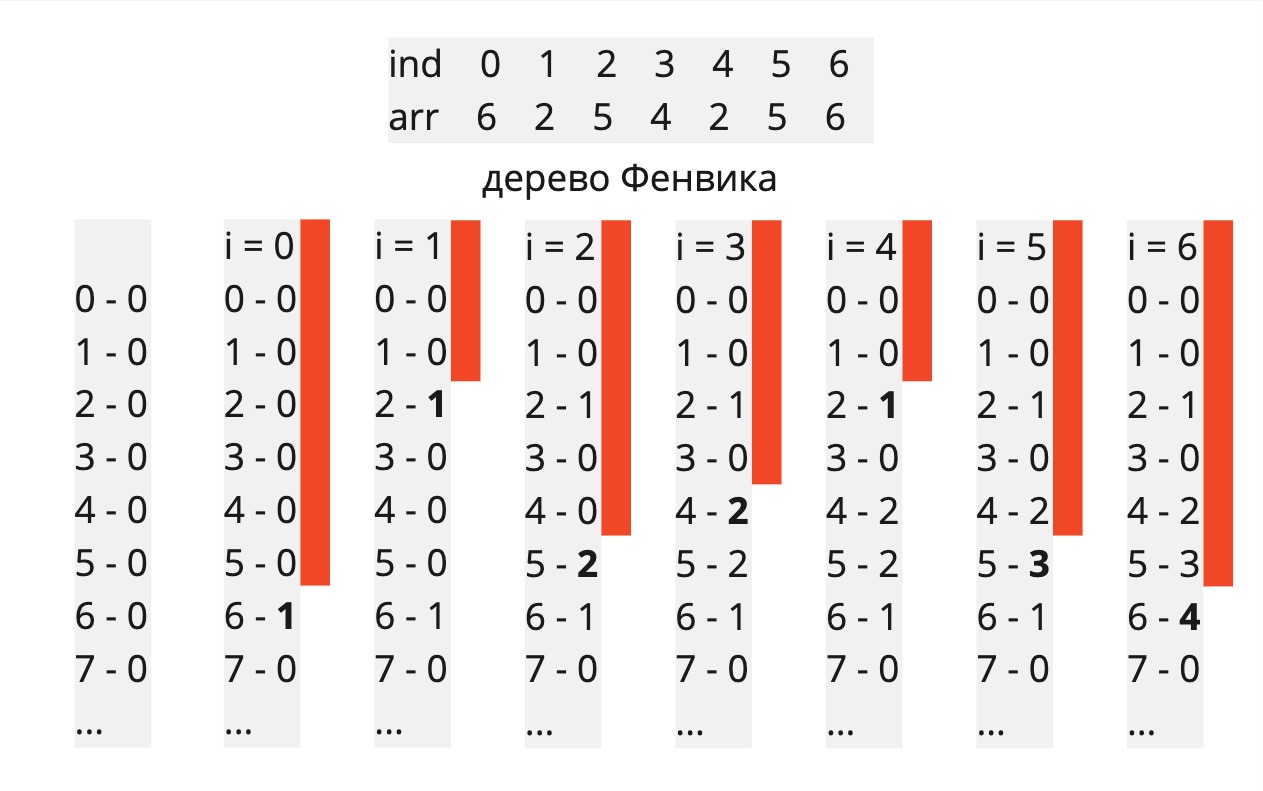
Important notein fact, the Fenwick tree array looks different, because not only one index is changed, but also several related ones using the function p(i) indexes, but to simplify things I drew this option.
Ninth task
Original condition
Given a sequence of n numbers. It is necessary to find the number of increasing subsequences of the greatest length of a given sequence a1, . . . , an. Since this number can be quite large, it is necessary to find the remainder when dividing it by 10^9 + 7.
The same task can be found on LeetCode number 673
The solution is similar to the eighth problem, but we will store not only the length, but also the number of increasing subsequences.
The complete solution can be viewed at GitHub
Here, by the way, we are compressing numbers, since the Fenwick tree cannot work with negative indices.
Tenth task
Condition
Given an array of n elements. You need to find the number of inversions in it. Inversion is such indexes i And jWhat i < j And arr[i] > arr[j]
To solve this problem, we will use a Fenwick tree for the sum. With each iteration, we will receive the number of elements (sum) that are to the right of the current number. How it works?
At a certain point in time (at index j) we have added elements in the tree whose index is less than j. All that remains is to find the number of elements that are greater arr[j]. This is exactly what is written in the problem statement.
The code looks something like this, but here importantwhat if the numbers exceed 10^6 they will need to be compressed.
class fenwick {
public:
vector<int> f;
explicit fenwick() {
f.resize(1000001, 0);
}
int sm(int x) {
int result = 0;
for (; x >= 0; x = (x & (x + 1)) - 1) {
result += f[x];
}
return result;
}
int sum(int l, int r) {
if (l) return sm(r) - sm(l - 1);
else return sm(r);
}
void inc(int i) {
for (; i < 1000001; i |= i + 1) {
f[i]++;
}
}
};
int main() {
int n;
cin >> n;
vector<int> arr(n);
for (int i = 0; i < n; ++i) cin >> arr[i];
fenwick tree;
int ans = 0;
for (int i : arr) {
auto q = tree.sum(i + 1, 1000000);
ans += q;
tree.inc(i);
}
cout << ans;
return 0;
}
Eleventh task
Original condition
The Romans are advancing again. This time they are much more numerous than the Persians, but Shapur is ready to defeat them. He says, “A lion will never be afraid of a hundred sheep.”
Despite this, Shapur must find the weakness of the Roman army in order to defeat it. As you remember, Shapur is a mathematician, so he determines how weak an army is, like a number – the degree of weakness.
Shapur believes that the degree of weakness of the army is equal to the number of such triplets i, j, kWhat i < j < k And a[i] > a[j]> a[k]Where a[x] – the strength of a person standing in line at place number x.
Help Shapur find out how weak the Roman army is.
Restatement
Given an array of integers of size n. It is necessary to find the number of index triplets i, j, ksuch that i < j < k And a[i] > a[j]> a[k]
Generalization
Given an array of integers of size n. It is necessary to find the number of superinversions of size k. That is, the same as with threes, but instead of three there can be k
The problem is very similar to the tenth problem. The idea is that if we know how many two-inversions were to the right of the current number, then we can know the number of three-inversions. From a dynamic programming point of view it would look like this:a = 6 4 5 12_i = 0 1 1 33_i = 0 0 0 2
Where 2_i is an array where 2_i[j] is the number of two-inversions that end at this index. 3_i similar, but with three inversions.
Array 3_i is built on the basis 2_i, 2_i is built on the basis a. Essentially, at each iteration in each array we are looking for the number of elements that are greater than the current one. For example 2_i[3] is the number of elements that are greater a[3]but which are to the left 3 by index. A 3_i[3] is the number of elements that are greater a[3] and who have 2_i[j] Above zero.
Essentially, at each iteration it is necessary to look for the number of elements that are greater a[i]. If we solve through dynamic programming we get complexity O(kn^2)since we calculate the whole array of dynamics k times, and at each iteration we go from 0 to i. This can be solved using a Fenwick tree with a similar idea to the tenth problem. It’s just that in this case we will need to use not one tree, but k trees.
The solution to the original problem can be found at GitHub
Twelfth task
Condition
Given an array arr integers of size n. Required m requests. Each request looks like this:
min(l,r)– it is necessary to find the minimum on the segment fromlbeforer - 1and return her. Formally: `min(l,r) = min(a[l],a[l + 1]…, a[r – 1])
Note that there are no array modification operations here. Such problems are solved in two parts. The first is preprocessing, when data is prepared in a special way. The second is the answers to the queries themselves.
Possible solutions:
Without preparation
Difficulty of preparation –
O(1)we do nothingQuery complexity –
O(n)in the worst case we go through all the elements
Segment tree
Enumeration of all options
Preparation –
O(n^2)we simply go through all possible segments and calculate the minimum for themRequest –
O(1)we will return pre-prepared data
Sparse tables
Sparse tables
We will look for the minimum for segments, but not all, but only for those segments whose length is a power of two. That is, conditionally we will have a two-dimensional array mWhere m[i][k] = min(a[i...i+2^k-1])
How to calculate values for such an array.
At
k = 0meaningm[i][0] = a[i]When moving from
kbeforek + 1:m[i][k + 1] = min(m[i][k], m[i + 2^k][k])
How can we now find the minimum on the segment? [l, r):
Заметим, что у любого отрезка имеется два отрезка длины степени двойки, которые пересекаются, и, главное, покрывают его и только его целиком. Значит, мы можем просто взять минимум из значений, которые соответствуют этим отрезкам.

Код выглядит примерно так. Здесь используется функция __lg, которая возвращает количество нулей до первой единицы в бинарной записи числа. Код взят с сайта алгоритмики
int a[maxn]mn[logn][maxn]; int rmq(int l, int r) { int t = __lg(r - l); return min(mn[t][l]mn[t][r - (1 << t)]); } memcpy(mn[0], a, sizeof a); for (int l = 0; l < logn - 1; l++) for (int i = 0; i + (2 << l) <= n; i++) mn[l+1][i] = min(mn[l][i]mn[l][i + (1 << l)]);
Thirteenth task
Given an array arr integers of size n. Required m requests. Each request looks like this:
add(l, r, v)- you need to add an element to everyone in the segment fromlbeforer - 1elementvget(i)- need to getielement
Let's build a segment tree for this problem. Now each node will store a value that needs to be added to the segment to which this node belongs.
To perform the addition, we need to divide our border into parts and add the value to the nodes related to these segments v. And to receive i element must go all the way from the root to the top i and collect the answer by adding the values.
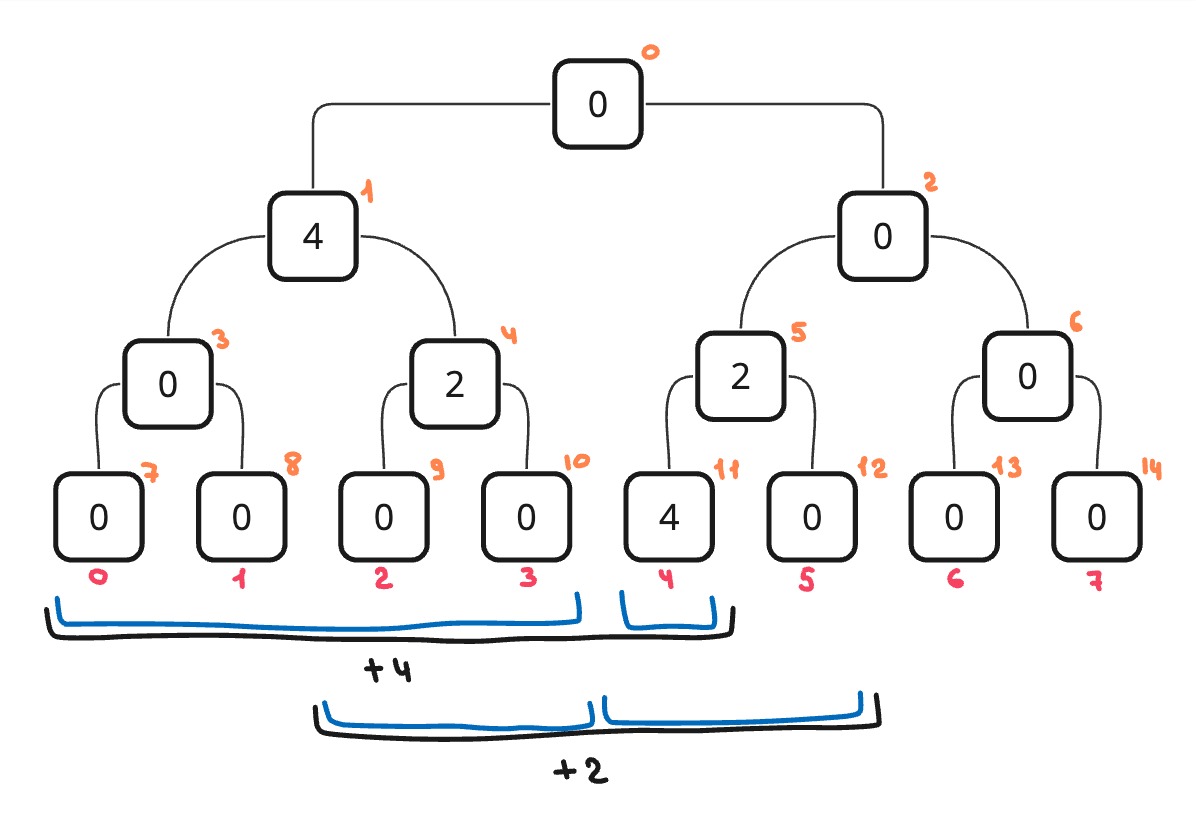
void resize(vector<int> &arr) {
int s = (int) arr.size();
int new_s = (int) pow(2, ceil(log2(s)));
arr.resize(new_s, 0);
}
vector<int> t;
void init(vector<int> &arr) {
resize(arr);
t.resize(arr.size() * 2, 0);
}
void add(int l, int r, int v, int x, int xl, int xr) {
if (l >= xr || xl >= r) {
return;
}
if (xl >= l && xr <= r) {
t[x] += v;
return;
}
int xm = (xl + xr) / 2;
add(l, r, v, 2 * x + 1, xl, xm);
add(l, r, v, 2 * x + 2, xm, xr);
}
int get(int i, int x, int xl, int xr) {
if (xl == xr - 1) {
return t[xl];
}
int xm = (xl + xr) / 2;
if (xm > i) {
return t[x] + get(i, 2 * x + 1, xl, xm);
} else {
return t[x] + get(i, 2 * x + 2, xm, xr);
}
}
There could be other tasks here...
Using a segment tree, you can combine several operations at once in one task, for example, assigning and adding on a segment and finding the maximum. Or XOR or OR and something else. You can also decide two-dimensional problems using a segment tree. But such topics are not very pleasant to describe, and they go beyond the basic understanding of the segment tree. You can view a few more problems on two-dimensional and multiple operations on a segment tree at GitHub
That's all, I hope the article was useful to someone 🙂





