How to measure the effectiveness of an investment portfolio: 3 practical approaches

Picture: Unsplash
Many novice investors evaluate the effectiveness of their asset portfolio solely on the basis of profit. This is not entirely true, because such an approach does not at all take into account the risk that accompanied the receipt of income.
Today we will talk about several approaches to assessing the effectiveness of the investment portfolio.
Trainor coefficient
It is a compound measure portfolio performance, which includes risk. At the same time, the author of the formula suggested that there are two risk components: the risk generated by fluctuations in the market, and the risk that arises from fluctuations in a particular asset.
The Trainor coefficient is also called the coefficient of remuneration to volatility – it is an indicator of profitability that exceeds the yield that could be obtained from risk-free investments for each unit of the market. An important point: when calculating the coefficient, the profitability is correlated only with the systematic risk, and not with the general one.
That is, the higher the Treynor coefficient, the more effective the investment portfolio. This coefficient is calculated as follows:
Where:
ri= portfolio return
rf= risk-free interest rate
β = beta (risk factor)
A.
Portal Investopedia leads An example of using the Trainor coefficient in real investments. It can be assumed that the ten-year yield of the S&P 500 index (market portfolio) is 10% per annum, and the average annual income from US treasury bonds (as a replacement for the risk-free interest rate) is 5%. Also, suppose there are three portfolio managers who have shown the following 10-year results
| Managers | Average annual return | Beta |
|---|---|---|
| A | 10% | 0.90 |
| B | 14% | 1,03 |
| C | fifteen% | 1.20 |
The Trainor coefficient for each of them will be as follows:
| Calculation | Trainor coefficient | |
| T (market) | (0.10-0.05) / 1 | 0.05 |
| T (manager A) | (0.10-0.05) /0.90 | 0.056 |
| T (manager B) | (0.14-0.05) /1.03 | 0,087 |
| T (manager C) | (0.15-0.05) /1.20 | 0,083 |
The higher the ratio, the more efficient the portfolio. Thus, if you only rely on profitability, then manager B seems to be the most productive. But if you evaluate the risks associated with his activities, it turns out that in fact, manager B showed the best result.
Sharpe Ratio
This measure is very similar to the Treynor coefficient, but here the risk is the standard deviation of the portfolio, and not the systematic risk presented by the beta.
The formula for calculating the Sharpe ratio is as follows:
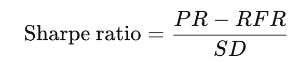
where
PR = portfolio return
RFR = risk-free interest rate
SD = standard deviation
A.
Using the example from the previous section, the S&P 500 has a standard deviation of 18% over a ten-year period. Then for portfolio managers, the Sharpe ratio will look like this:
| Manager | Annual return | Portfolio Standard Deviation |
|---|---|---|
| X | 14% | 0.11 |
| Y | 17% | 0.20 |
| Z | 19% | 0.27 |
| S (market) | (0.10-0.05) /0.18 | 0.278 |
| S (managerX | (0.14-0.05) /0.11 | 0.818 |
| S (manager Y) | (0.17-0.05) /0.20 | 0.600 |
| S (manager Z) | (0.19-0.05) /0.27 | 0.519 |
As in the previous case, it turns out that the best portfolio is not necessarily the one that brings the most money. On the contrary, the best result is profitability combined with acceptable risk.
In contrast to the Trainor coefficient, the Sharpe coefficient evaluates performance taking into account diversification. Thus, this measure is better suited for evaluating well-diversified investment portfolios.
Jensen coefficient
This measure is calculated using the CAPM model (Capital Asset Pricing Model), in Russian it is also called the model for assessing long-term assets. Its essence is that the required return on invested funds is determined not so much by the specific risk of the asset, but by the overall risk level of the entire market as a whole.
The Jensen coefficient ultimately calculates the excess return that the portfolio brings in excess of the expected return. This measure of profitability is called alpha.
Simply put, Jensen’s coefficient measures how much portfolio returns are related to the portfolio manager’s ability to generate results above the market average, taking into account risk. The higher the ratio, the better the risk-adjusted return. A portfolio with consistently positive higher-than-expected returns will have positive alpha, and vice versa.
The calculation formula looks like this:![]() ,
,
Where
PR = portfolio return
CAPM = risk-free interest rate + β (return on market risk-free interest rate)
Assuming a risk-free interest rate of 5% and a market yield of 10%, what will be the alpha of the following portfolios?
| Manager | Annual return | Beta |
|---|---|---|
| D | eleven% | 0.90 |
| E | fifteen% | 1.10 |
| F | fifteen% | 1.20 |
The calculation of expected portfolio returns is as follows:
| ER (D | 0.05 + 0.90 (0.10-0.05) | 0.0950 or 9.5% return |
| ER (E) | 0.05 + 1.10 (0.10-0.05) | 0.1050 or 10.5% return |
| ER (F) | 0.05 + 1.20 (0.10-0.05) | 0.1100 or 11% return |
Alpha is calculated by subtracting the expected return from the actual return:
| Alpha d | 11% – 9.5% | 1.5% |
| Alpha e | 15% – 10.5% | 4,5% |
| Alpha f | 15% – 11% | 4.0% |
What portfolio and its manager showed the best results? Manager E proved to be the best, because even though manager F showed the same level of return, the expected return in case of E was lower and the beta of the portfolio was much lower than in the case of portfolio F.
An important point: the assessment of profitability and risk for stocks and portfolios will change over time. The Jensen coefficient requires the use of different risk-free rates for each interval. That is, to evaluate productivity over a five-year period using annual intervals, you will also need to study the annual yield minus the risk-free income for each year and correlate it with the annual yield of the market portfolio minus the same risk-free rate.
Useful links on the topic of investment and stock trading:
- Open a brokerage account online
- Test account with virtual money
- Software for trading on the exchange: trading terminal, mobile applications
- Structural Products
- Model Portfolios
Read reviews, market analytics and investment ideas in Telegram channel ITI Capital






