two statistics with similar names but different meanings

I teach a course on statistical thinking to masters, and one topic causes obvious difficulties for them – how the standard deviation differs from the standard error and in what cases to apply this or that statistics. I think it will be interesting to talk about this on the LANIT blog.

*I used an Excel file for illustration. In it you will find formulas, dynamic data based on volatility functions, and static data used as the basis for drawings and calculations for the note. The file displays correctly in Excel 2016 or later.

*For illustration I used Excel file. In it you will find formulas, dynamic data based on volatility functions, and static data used as the basis for drawings and calculations for the note. The file displays correctly in Excel 2016 or later.

Random variables

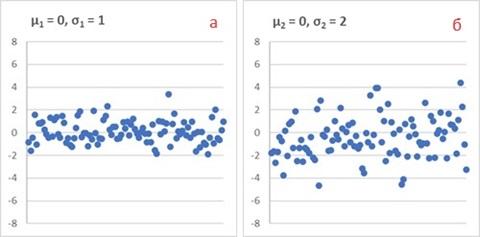
Let X – random normally distributed variable. Its mathematical expectation in probability theory is denoted M[X] or E[X]and in statistics – μ. Let's create two samples of 100 values ​​each. To generate samples in Excel, we use the formula =NORM.REV(RAND();μ;σ). Let's set the same expectations μ_1 = μ_2 = 0 and different standard deviations: σ_1 = 1And σ_2 = 2.

Rice. 1. Normally distributed random variables. The abscissa axis is the number of the element in the sample, the ordinate axis is the value of a normally distributed random variable. It can be seen that an increase in the standard deviation leads to a greater scatter of points.

Rice. 1. Normally distributed random variables. The abscissa axis is the number of the element in the sample, the ordinate axis is the value of a normally distributed random variable. It can be seen that an increase in the standard deviation leads to a greater scatter of points.

Arithmetic mean of the sample

Despite the fact that we have set the expectation for the generating process μ = 0, the sample average will differ from this value. The sample average is called arithmetic mean \bar{x} (or just average), and calculated using the formula:

(1)\bar x=\frac1n \displaystyle\sum_{i=1}^{n} x_i

Where x_i – individual values ​​of a random variable, n – number of random variable values ​​in the sample.

For the samples in Fig. 1 it turned out that \bar x_1 = 0.102, \bar x_2 = -0.445.

Dispersion and standard deviation of the population

To measure the dispersion (variability) of a random variable relative to its expectation, the dispersion is most often used, denoted D[X] , Var[Х]or σ^2

(2) σ^2=\frac1n\displaystyle\sum_{i=1}^{n} (x_i-μ)^2

… and standard deviation σ

(3)σ=\sqrt {σ^2}=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-μ)^2}}{n}}

Sample standard deviation

Standard Deviation (SD) s calculated by the formula:

(4)s=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n}}

In general, terms are used slightly differently by different authors. I like the following approach. The population is described parametersdenoted by Greek letters: mathematical expectation μ and standard deviation σ . Samples describe statisticiansdenoted by Latin letters: arithmetic mean \bar{x} and standard deviation s .

In real life, no mathematical expectation μnor standard deviation σ general population are unknown. But by extracting a sample, we learn something about expectation and standard deviation. They say it's average \bar{x} is assessment mathematical expectations μand the standard deviations – assessment standard deviation σ.

When generating a random variable, we set σ_1 = 1 And σ_2= 2. For the samples in Fig. 1 received s_1 = 0.985, s_2 = 1.824.

The less s, the more closely the values ​​are located around the average. So,

standard deviation – a measure of the spread of data in a sample

Standard Deviation of Sample Means

Let us now focus on the process of generating random numbers with μ = 0 And σ = 1. Let's extract not just one sample, but several. Although the arguments μ And σ random number generator are constant, the random process will lead to different values \bar{x} for individual samples:

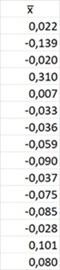
Rice. 2. Average values ​​for 15 samples of size

Rice. 2. Average values ​​for 15 samples of size n = 100

If we take not 15, but 1000 samples, we can build a fairly smooth distribution of average values \bar{x}:

Rice. 3. Distribution of average values ​​for 1000 samples of size . The x-axis is the range of average sample values, the y-axis is the proportion of such samples

Rice. 3. Distribution of average values \bar{x} for 1000 samples of size n=100 . The x-axis is the range of average sample values, the y-axis is the proportion of such samples

Set of averages \bar{x}_i can be considered as a random variable \bar{X}. For its distribution (Fig. 3), you can also calculate the standard deviation using formula (4): s_{\bar{X}} = 0.1. Subscript \bar{X} indicates that the standard deviation refers to the average values \bar{x}_i. Note that the standard deviation of one sample (Fig. 1a) was equal to s_1 = 0.985 . The standard deviation of each sample is given by the generating process, in which the standard deviation of the population σ_1 = 1. For average values ​​of samples of size n = 100 standard deviation s_\bar{X} approximately 10 times less than for individual values ​​in the sample s_1.

Let's calculate the standard deviation for 100 samples of other sizes n = 3, 5, 10, 20. It turns out that the standard deviation of the means depends on the sample size:

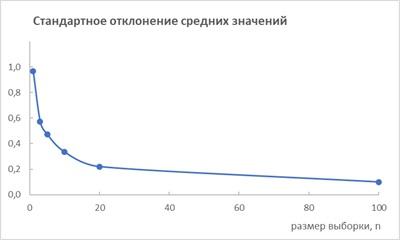
Rice. 4. Dependence of standard deviation of average values ​​on sample size

Rice. 4. Dependence of standard deviation of average values ​​on sample size

Let us derive the formula for this dependence.

Standard error formula

To begin with, we will show that the constant factor can be taken out of the dispersion sign by squaring it.

By definition, varianceVar random variable X equal to

(5)Var(X)=E[(X-E[X])^2]

Where E[X] – mathematical expectation of a random variable X,E[(X-E[X])^2] – mathematical expectation of the squared difference between the random variable itself and its expectation.

Let us now consider the random variable Y = cXWhere c – constant. Let's find the variance Y

(6)Var(Y)=E[(Y-E[Y])^2]=E[(cX-E[cX])^2]=E[c^2(X-E[X])^2]=c^2E[(X-E[X])^2]=c^2Var(X)

On the other hand, the arithmetic mean for the sample:

(7)\bar{x}={\frac{x_1+x_2+…+x_n}{n}}

Sample variance:

(8)Var(\bar{x})=Var({\frac{x_1+x_2+…+x_n}{n}})=\frac{1}{n^2}Var(x_1+x_2+…+x_n)

Here we have taken advantage of the property (6) we just derived, using c = 1/n .

Now let’s take into account that the variance of the sum of independent random variables is equal to the sum of their variances:

(9)Var(\bar{x})=\frac{1}{n^2}Var(x_1+x_2+…+x_n)={\frac{Var(x_1)+Var(x_2)+…+Var( x_n)}{n^2}}

Let us take into account that all random variables x_i equally distributed:

(10)Var(\bar{x})={\frac{Var(x_1)+Var(x_2)+…+Var(x_n)}{n^2}}={\frac{nVar(x)}{ n^2}}={\frac{Var(x)}{n}}

By taking the root and moving from the population parameter to the sample statistics, we can write the standard deviation of the random variable \bar{X}:

(11)s_{\bar{X}}={\frac{s_1}{\sqrt{n}}}

We obtained the dependence of the standard deviation of the average values ​​of the samples s_{\bar{X}} from standard deviation of single values s_1 and sample size n. If we substitute (4) into (11), we get:

(12)s_{\bar{X}}=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n^2} }

Sizes_{\bar{X}}called standard error or standard error of the mean. s_{\bar{X}} allows you to estimate from one sample in what range from the sample average \bar{x} the mathematical expectation of the general population is found μ. For example, in the range {\bar{x}} ± 2s_{\bar{X}} the expectation of the general population will hit with a probability of 95%.

If the standard deviation is an indicator of the variability of elements in a sample, then the standard error is a similar indicator (calculated using the same formula) of the variability of sample means.

So,

standard error – a measure of the mathematical expectation of the population μ based on the sample mean \bar{x}.

Note that as sample size increases n the standard error will decrease. In the limit at n → ∞, x̅ → μ And s_\bar{X} → 0.

Biased and unbiased estimates

The estimate of the population parameter in the general case can be represented by the equation:

(13) Estimate = Estimated Population Parameter + Bias + Noise

It turns out that the arithmetic mean is an unbiased estimate of the expectation:

(14) \bar{x} = μ + Noise

To illustrate this point, I randomly assigned 10,000 numbers ranging from 0 to 100. And then created 100 samples of 100 consecutive values: from 1 to 100, from 101 to 200, etc. The average value for all 10,000 random numbers is plotted on the graph in the form of a dotted line, as well as the moving average for a sequence of samples in the form of dots. For example, the first point is the arithmetic mean for the first sample: 1…100, the second point is the statistical average of two samples: 1…100 and 101…200, etc.

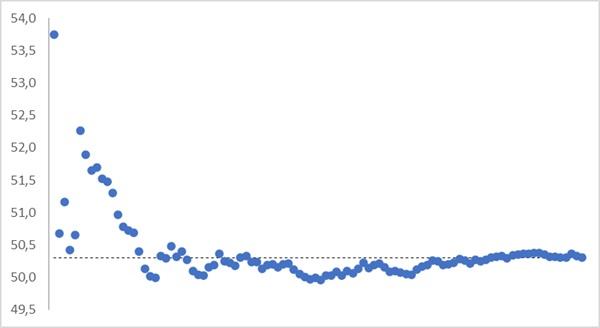
Rice. 5. The arithmetic mean, as an unbiased estimate of the expectation. It can be seen that the average of the samples tends to the average of the entire population.

Rice. 5. The arithmetic mean, as an unbiased estimate of the expectation. It can be seen that the average of the samples tends to the average of the entire population.

It seems paradoxical, but the standard deviation turned out to be a biased estimate of the standard deviation:

(15) s = σ + Bias + Noise

Rice. 6. Standard deviation as a biased estimate of the standard deviation

Rice. 6. Standard deviation as a biased estimate of the standard deviation

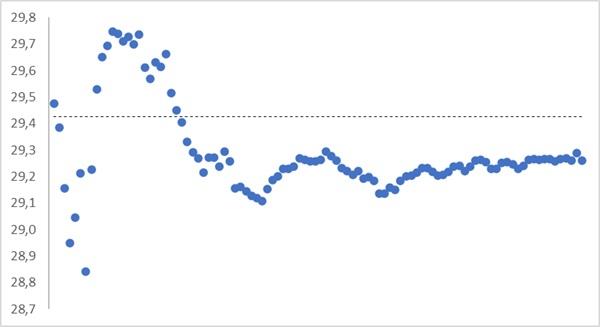
A sample estimate of the standard deviation, which we called the standard deviation, and introduced by formula (4) gives a systematic error!

Bessel amendment

To understand the source of systematic error, we once again present the formulas for root mean square and standard deviation.

(3)σ=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-μ)^2}}{n}}(4)s=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n}}

… and let's return to the example in Fig. 1a.

We know (we set it ourselves in Excel) that the expectation of the general population μ = 0 . But the arithmetic mean of the sample \bar{x}=0.102 . And this is our best estimate of the expectation. Correct (unbiased) estimate of the population standard deviation σ should be based on deviations from μ = 0 according to formula (3). But if we don't know the true meaning μ then we calculate the standard deviation s from \bar{x} according to formula (4).

notice, that μ in formula (3) can be represented as \bar{x}– sWhere c – a constant (bias) indicating how much the sample mean differs from the expectation of the general population. Then x_i – μ can be replaced by x_i – \bar{x} + s. Let's denote the difference x_i – \bar{x}one character a_i. In formula (4) we are looking for the sum a_i^2and in formula (3) – the sum (a_i + c)^2. But

(16) (a_i + c)^2 = a_i^2 + 2a_ic + c^2

By definition, the sum of the second terms over the sample Σ2a_ic is equal to zero – deviations from the average in different directions compensate each other. That's why it's average. Sum a_i^2 is the sum of the squares of the distance from the sample values ​​to the sample mean. c^2– the sum of squared distances between the arithmetic mean of the sample and the expectation of the general population.

Because the c^2positive (except when \bar{x} = μ) the sum of the squares of the distance from the sample values ​​to the population expectation will always be greater than the sum of the squares of the distance to the sample mean.

That's why s gives a systematic error (downward) compared to σ.

In a biased estimate s, By using the sample mean instead of the expected value, we underestimate each x_i-\bar{x} on \bar{x} – μ.

To find the discrepancy between the biased estimate s and population parameter σwe need to find the expectation E(\bar{x} – μ). In chapter Standard error formula we showed that this expectation is equal to the variance of the sample mean σ/n. Thus, the biased estimate underestimates σ on σ/n:

(17) biased estimate =(1-\frac1n) * unbiased estimate =\frac {n-1}{n}* unbiased estimate

The Bessel correction is the coefficient (18)\sqrt{\frac{n}{n-1}} by which the standard deviation should be multiplied to make the biased estimate unbiased:

(19)s_{unbiased}=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n}} ∙ \sqrt{\ frac{n}{n-1}} =\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n-1}}

Let's check the behavior s_{unbiased} on model:

Rice. 7. Standard deviation as an unbiased estimate of the standard deviation

Rice. 7. Standard deviation as Notbiased estimate of standard deviation

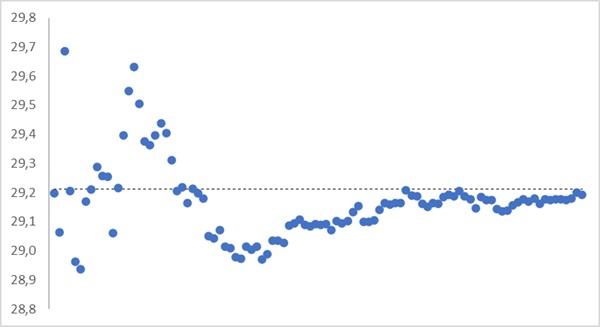
The Bessel correction should also be introduced into formula (12) to calculate the standard error of the mean. We get:

(20)s_\bar{X}=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n^2}} * \sqrt{\frac{n}{n-1}} =\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n (n-1)}}

Assumptions

When deriving the standard deviation and standard error formulas, we used the following assumptions, either explicitly or implicitly:

  • the data in the sample is subject to normal distribution;

  • sample is representative for the general population;

  • observations in the sample independent from each other; for time series, the assumption of independence is usually violated;

  • measurements are carried out on interval or relative scale; the use of categorical data may be incorrect;

  • assessments sensitive to emissions.

Let's see what happens when one or more assumptions are violated.

Distributions with fat tails

The normal distribution has a thin tail. This means that the behavior of a normally distributed random variable is determined by the central part of the distribution. Tail values ​​are very rare. Central limit theorem gives fast convergence, and we observe characteristic behavior as in Fig. 5.

In response to my query, ChatGPT pointed out three areas where the data is well described by a normal distribution: human height, measurement errors (of length or mass among a homogeneous group of objects), intellectual ability (IQ tests are designed to fit a normal distribution, and average intelligence tends to fall in the middle distributions).

The normal distribution is so widespread that we use it even when we shouldn’t – when working with financial instruments, economic and social phenomena. A typical example is the average income of bar patrons, which will skyrocket to a billion if Bill Gates happens to walk in there.

Let's see how a random variable defined by the standard Cauchy distribution converges to the mean:

(21) f(x)=\frac{1}{π(1+x^2)}

To model in Excel, I took advantage of the fact that the Student t-distribution with the number of degrees of freedom df = 1 is equivalent to the standard Cauchy distribution. And for t-Student in Excel there are formulas for direct and inverse distributions.

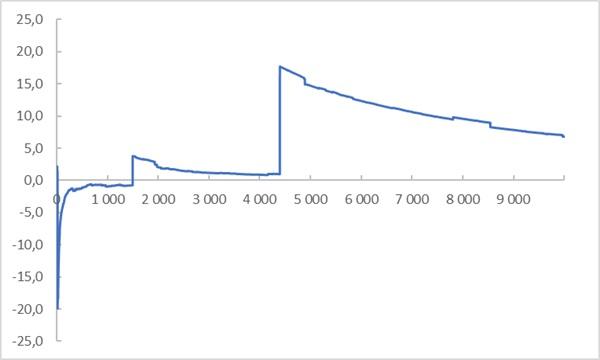
Rice. 8. There seems to be convergence of the Cauchy distribution... but only until the next outlier

Rice. 8. There seems to be convergence of the Cauchy distribution… but only until the next outlier

If we look at the assumptions stated above, we see that Cauchy distributed data violates almost everything. (1) No sample is representative. The tail values ​​are still relatively rare (though not as rare as in a normal distribution), but they determine the sample average. (2) Presence or absence emission in a sample, the arithmetic mean has a stronger effect than central tendency.

Following the arithmetic mean, both the standard deviation and the standard error obtained from a sample tell little about the population.

I used the extremely fat-tailed Cauchy distribution as an example, but many other distributions, such as power-law ones, behave only slightly more predictably. This topic is covered in detail in Nassim Taleb's new book (see link below).

Areas of use

Here are some uses of standard deviation:

  • Estimation of data scatter (variability) relative to the average value. The larger the standard deviation, the greater the spread.

  • Quality control as an indicator of variability in the production or management process. A smaller standard deviation indicates a more stable process. Standard deviation can be used to plot boundaries Shewhart control charts.

Areas of use of Standard Error of the Mean (SEM):

  • Confidence intervals for the mean. For example, if you conducted a survey with a small sample and calculated the mean and SEM, you can construct a confidence interval indicating where the true mean lies in the population.

  • When comparing average values ​​from different samples SEM is used to determine the statistical significance of differences between samples. If the difference in means is greater than a few SEMs, it may indicate a statistically significant difference.

  • SEM indicates how accurate The sample mean estimates the true mean of the population. A large SEM indicates greater uncertainty in the estimate.

With caution and reservations, standard deviation and standard error should be used to assess risk in the financial sector. The SD and SEM formulas are based on several statistical assumptions. It is important to understand these assumptions when using and interpreting the results.

Literature

  1. Vladimir Gmurman. Theory of Probability and Mathematical Statistics

  2. Bessel amendmentBessel's correction

  3. Nassim Nicholas Taleb. Statistical implications of fat tails.

Similar Posts

Leave a Reply

Your email address will not be published. Required fields are marked *