Schwartz's boot is a paradoxical "cylinder" that can have an infinite area

Greetings! Today I want to talk about a geometric object that looks like a paper lantern, but is actually a very interesting counterexample in the field of finding the area of polyhedra. So let’s go!

Stair Paradox

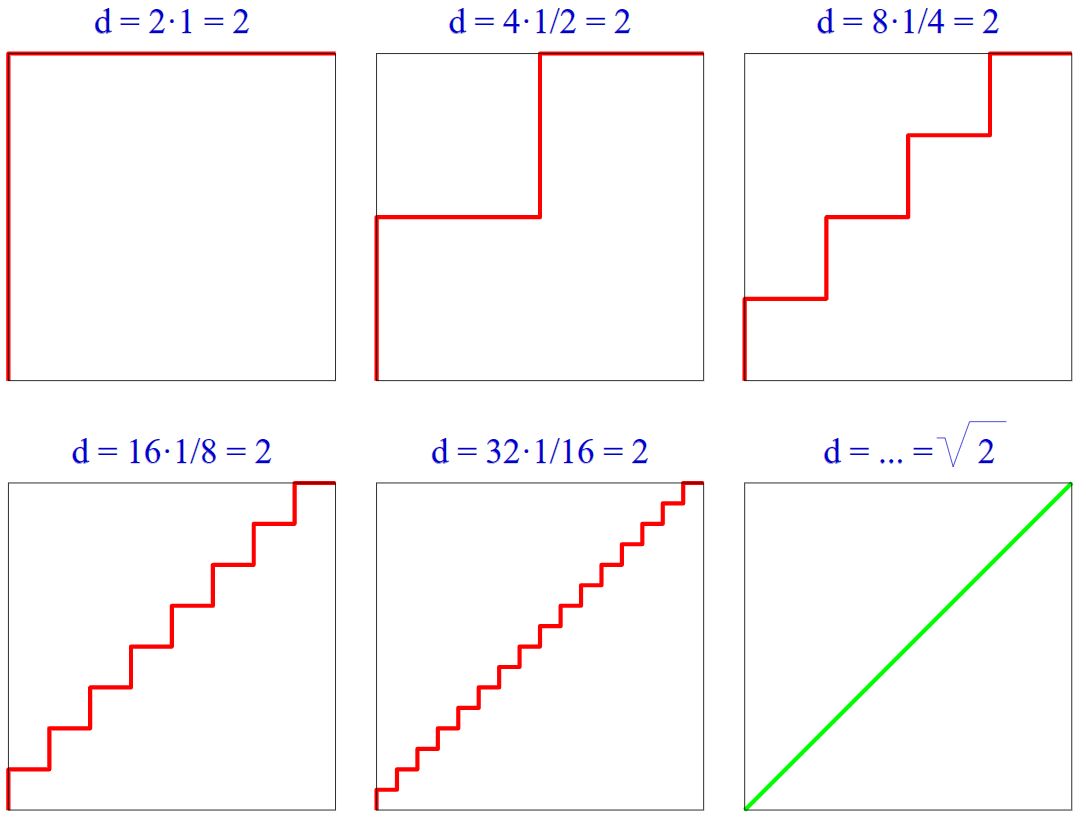
Archimedes approximately determined the circumference of a circle using the lengths of the sides of inscribed and circumscribed regular polygons. In a general sense, the length of any curve can be expressed as the largest value of the lengths of the inscribed broken lines. However, for this method to work correctly, the polyline vertices must be on the curve itself, and not just next to it.

Otherwise, as shown in the so-called “ladder paradox”, broken lines consisting of vertical and horizontal segments with a total length of 2 can be located so close to a diagonal segment of length √2 that they will “visually” converge to the diagonal, but will have different length.

Boot Schwartz provides a similar counterexample for surface area, demonstrating that more than just the condition that the vertices lie on the desired surface is required to accurately approximate the area.

At the end of the 19th century, the German mathematician Hermann Schwartz (1843-1921) developed his own construction, which served as a counterexample to the erroneous definition presented in J. A. Serret’s 1868 book A Course in Calculus and Integral. This book stated that:

Let a part of the curved surface be bounded by the contour C; we define the area of this surface as the limit to which S tends the area of the inscribed polyhedral surface formed of triangular faces and bounded by the polygonal contour Γ of which the contour C is the limit. It is necessary to show that the limit S exists and that it does not depend on the law according to which the faces inscribed polyhedral surface are compressed.

It is stated, for example, that the area of the relief in the picture above will always be the same (by calculation), regardless of how the surface is triangulated (size, angles, number of triangles)

Schwartz boot design

Schwartz developed a method for approximating surfaces using antiprisms. The first parameter of the antiprism, we denote it as “m”represents the number of circles, the second parameter, let’s denote it as “n”, represents half the number of triangles in each ring of this structure. For the case with one ring (m=1) the resulting surface is formed from triangular faces constituting an antiprism of order n.

An antiprism is a semi-regular polyhedron, in which two parallel faces (bases) are regular n-gons equal to each other, and the side faces are regular triangles. There are 34 triangles in the figure, so n=17, m=1

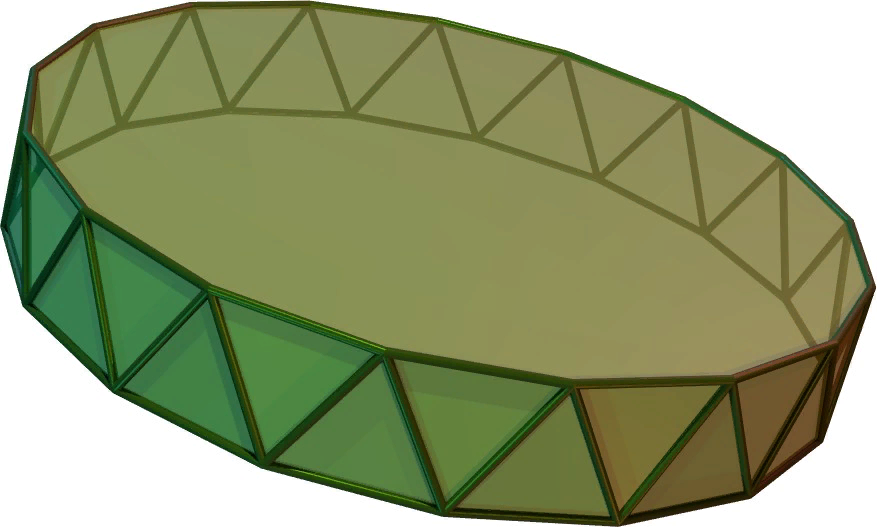
At higher values of m, the Schwartz boot is formed by arranging m such antiprisms.

To construct a Schwartz boot that approximates a given regular circular cylinder, the cylinder is cut into m pancakes. These pancakes have m+1 round borders – two at the ends of the cylinder and one more at the site of the cut. Distributed in each pancake n vertices, forming the correct n-gon (it is clear that the number of these angles can be increased, striving for similarity with a circle).

It looks very similar, doesn't it? — It looks very similar, doesn’t it?

These polygons are rotated by an angle π/n from one circle to the next, so that the edges of regular polygons and the nearest vertices on the next pancake form the base and vertex of an isosceles triangle. These triangles intersect from edge to edge, forming the polyhedral surface of the Schwartz boot, which is topologically equivalent to a cylinder.

Schwarz's boot with n = 10. Triangles of a pair of pancakes "convex" at an angle of 360/10 = 36 degrees. Thus, the smaller we make this angle, the more the surface of the Schwartz boot will be cylindrical. — Schwarz’s boot with n = 10. The triangles of a pair of pancakes are “convex” at an angle of 360/10 = 36 degrees. Thus, the smaller we make this angle, the more the surface of the Schwartz boot will be cylindrical.

Schwartz’s boot can be glued from a flat sheet of paper with triangle faces applied to it. This pattern of folds is called the Yoshimura pattern:

If we derive the formula for the surface area of a Schwartz boot, we get the following expression:

For a Schwartz boot with parameters m and n, each stripe is a shorter cylinder of length ℓ/m, approximated by 2n isosceles triangles.

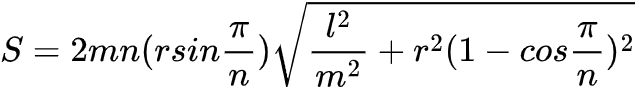
Paradox

If you calculate the limits sequentially, you will obviously get an excellent approximation to the surface area of a cylinder:

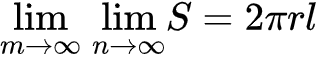
In this case, the inner limit already converges to the desired value, and the outer limit is redundant (in other words, it does not matter how many pancakes the cylinder is cut into, the entire approximation will occur due to a large number of triangles).

In this case, for a given value nwith increasing m and by decreasing the length of each cylindrical strip l/m, each of the corresponding strips of isosceles triangles becomes practically flat. The surface area of each pancake tends to a finite number, and since in the second limit we increase the number of pancakes indefinitely, the total surface area tends to infinity.

You can also establish a functional relationship between the parameters “m” And “n” and explore the limit while simultaneously increasing both parameters while maintaining this connection.

Various options for such a connection can lead to two possible scenarios: convergence in a certain area or divergence to infinity. For example, if you choose m = cn (Where c – an arbitrary constant) and consider the limit for large values n, then there will be convergence in a certain area. While setting m = cn³ will lead to divergence. The third type of restricted behavior is achieved when m = cn². For this choice of parameters, we obtain the formula:

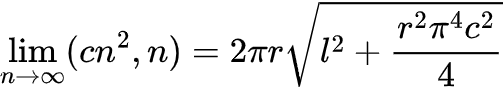
Playing with the value of c, you can get any value of the surface area. The above also highlights the importance of careful choice of triangulation for use in computer graphics and the finite element method used in scientific and engineering modeling. In the field of computer graphics, scenes are often represented as triangular surfaces, and the correct display of lighting depends on the orientation of the normals to the surface.

All volume calculations – in one article.

The wrong choice of triangulation method, like in the case of the Schwartz boot, can lead to the formation of a surface, like a folding accordion, with normals that are far from the normals of the original surface. Closely spaced sharp bends on this surface can also cause smoothing problems.

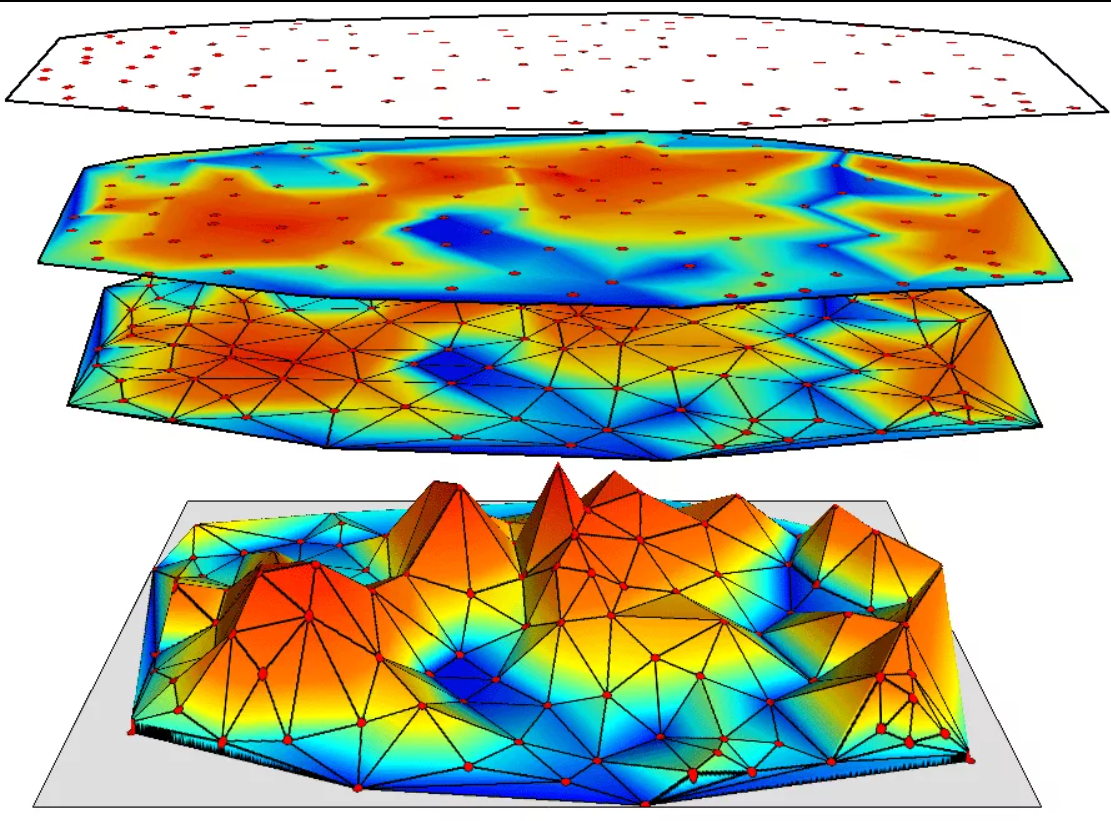
Problems arise when triangles with angles close to 180 degrees are included in the partition. In some classes of Schwartz boots that use angles limited to 180 degrees, the area converges to the same area as the cylinder as the number of triangles increases to infinity.

A triangulation created by a scientist to find a solution to the problem of the installation's magnetic field distribution. The colors indicate that the analyst has set the material properties for each zone, in this case, the spool of conductive wire is orange; the ferromagnetic component (possibly iron) is light blue in color; and gray air. Although the geometry may seem simple, writing down and solving equations for such a situation is almost impossible, which is why the finite element method has to be applied. — A triangulation created by a scientist to find a solution to the problem of the installation’s magnetic field distribution. The colors indicate that the analyst has set the material properties for each zone, in this case, the spool of conductive wire is orange; the ferromagnetic component (possibly iron) is light blue in color; and gray air. Although the geometry may seem simple, writing down and solving equations for such a situation is almost impossible, which is why the finite element method has to be applied.

The finite element method, in its basic form, approximates a smooth function (often representing a solution to a physical modeling problem in science or engineering) by replacing it with a piecewise linear function on triangulations. The Schwartz boot example demonstrates that even for simple functions such as the height of a cylinder above a plane passing through its axis, and even if the function values are known exactly at the vertices of the triangulation, using triangulation with angles close to 180 degrees can lead to significantly inaccurate simulation results.