New everywhere or statistical equivalence tests
Classical statistical tests are, as a rule, tests that test the hypothesis of equality (median to a certain value, averages in two independent groups, variance in many dependent groups, correlation coefficient zero, etc.).
However, for more than 30 years there has been an alternative approach developed in the course of research in psychology – equivalence tests. It is based on the idea, for example, that some non-zero correlation value can still be considered insignificant for a particular problem being solved.
In R, the negligible package is responsible for implementing tests of this type. Let’s consider different practical tasks step by step, add a pinch of theory and calculations to each.
1) Correlation tests based on equivalence (for normally distributed quantities)
Full explanation in Goertzen, J. R., & Cribbie, R. A. (2010). Detecting a lack of association. British Journal of Mathematical and Statistical Psychology, 63(3), 527–537
In short: we test two null hypotheses at once in the form –r* < r and r > r*, where r* is the margin of insignificance of the correlation coefficient established by us, r is the correlation coefficient according to our data.
Practice: take the CASchools database and test the hypothesis that the correlation coefficient between test scores in math and reading is in the range of insignificance [-0,2 ; 0.2]
library(AER)
library(negligible)
library(tidyverse)
data(CASchools)
CASchools <- as.data.frame(CASchools)
neg.cor(v1 = CASchools$math, v2 = CASchools$read, eiU = .2, eiL = -.2)
The boundaries of the range of insignificance are set by the user, based on the task, and can be different. The algorithm outputs:
– the value of the correlation coefficient: 0.9229;
– 95% confidence interval for it, calculated on the basis of the bootstrap;
– conclusion on the null hypothesis (in our case, the hypothesis of the insignificance of the correlation coefficient is rejected).
2) Proportions equivalence test (2 by 2 test)
Practice: take the CASchools database and test the hypothesis about the equivalence of proportions in the table for two variables – the grading system used (CC-06 or CC-08) and the excess of the median score in mathematics
v1<-as.vector(CASchools$math>median(CASchools$math))
v2<-as.vector(CASchools$grades)
tab<-table(v1,v2)
tab
neg.cat(tab=tab,alpha=.05,eiU=0.5,nbootpd=50)
The algorithm outputs:
– the value of the classical Cramer’s criterion and its 95% confidence interval;
– comparison of the upper value of the Cramer coefficient and the user-specified value of insignificance;
– conclusion on the null hypothesis (in our case, the hypothesis of the insignificant difference in proportions is accepted).
3) Test for the presence of the influence of the third variable on the correlation between the other two.
Read more in the article at http://doi.org/10.20982/tqmp.16.4.p424
In short: two models of the relationship between variables are built:

It is necessary to understand whether there is a relationship between X and Y, or whether it is all due to the fact that both of these variables are correlated with some other variable M.
Practice: Take the CASchools database and test the hypothesis that the correlation coefficient between math and reading test scores is due to the number of computers.
neg.esm(X = math,Y = read,M = computer,eil = -.15,eiu = .15,
nboot = 50,data = CASchools)
The final conclusion from the two procedures applied is that the null hypothesis that the direct effect of the variables (the difference between the total and indirect effect) is not negligible cannot be rejected. That is, the magnitude of the direct influence of the variables is not included in the default interval [-0.15 ; 0.15].
4) Test of equivalence of variances in independent samples.
Read more in the article at https://doi.org/10.1080/00220973.2017.1301356
Practice: take the CASchools database and test the hypothesis that the dispersion of math grades among students graded differently does not differ significantly
neg.indvars(dv = CASchools$math, iv = CASchools$grades, eps = 0.25)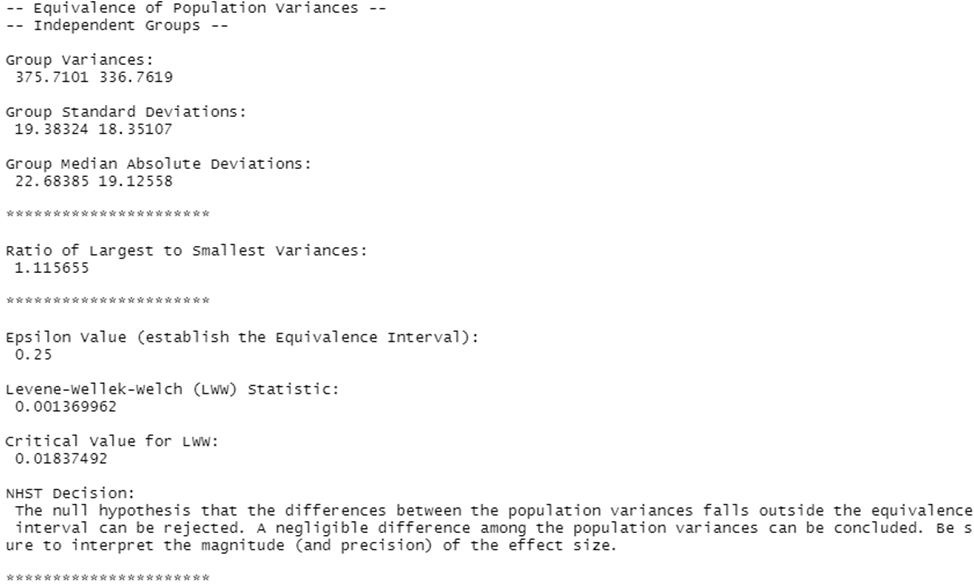
The final output includes:
– values of group variance, standard deviation and absolute median deviation
– calculated value of the ratio of variances
– test statistics and conclusions on it (in our case, the hypothesis that the magnitude of the difference between the population variances goes beyond the equivalence interval can be rejected).
A significant difficulty in the widespread use of this test is the isolation from the specific values of a specific indicator of the eps value, which determines the “rigidity” of the test. There is only a recommendation in one article to use a value of 0.25 if you want a conservative test, and a value of 0.5 if you want a liberal one.
5) Test for the insignificance of the difference in mean values in dependent groups
Practice: take the PSID7682 dataframe and test the wage equivalence hypothesis in 1976 and 1982
data("PSID7682")
date <- rbind(PSID7682[PSID7682$year==1976,c(13,12,14)],PSID7682[PSID7682$year==1982,c(13,12,14)])
neg.paired(outcome = date$wage, group = date$year, ID = date$id,eil=-10,eiu=10)
The final output is very detailed – the averages, variances, standard deviation, absolute median deviation by groups are displayed. In essence, the hypothesis being tested can be said as follows: the null hypothesis that the difference between the means exceeds the equivalence interval (which is specified by the parameters eil and eiu) cannot be rejected.
6) Equivalence test for the insignificance of the influence of the predictor in the regression model
Practice: using the CASchools dataframe, we will build a model of the dependence of math scores on the number of teachers, computers and average income, check the significance of the predictor “number of teachers”
neg.reg(formula=math~teachers+computer+income,data=CASchools,predictor=teachers,eil=-.1,eiu=.1,nboot=50)
The final output shows the value of the coefficient at change, its 95% confidence interval. General conclusion: The null hypothesis that the regression coefficient is not insignificant can be rejected.
7) Test for the equivalence of two correlation coefficients in groups
Practice: using the CASchools dataframe, we will test the hypothesis of equivalence of correlations between scores in reading and mathematics for students with different grading systems
yx1 <- CASchools %>% filter(grades=="KK-06")
yx2 <- CASchools %>% filter(grades!="KK-06")
neg.twocors(r1=cor(yx1$math,yx1$read),n1=length(yx1$math),r2=cor(yx2$math,yx2$read),n2=length(yx1$math),eiu=.15,eil=-0.15, dep=FALSE)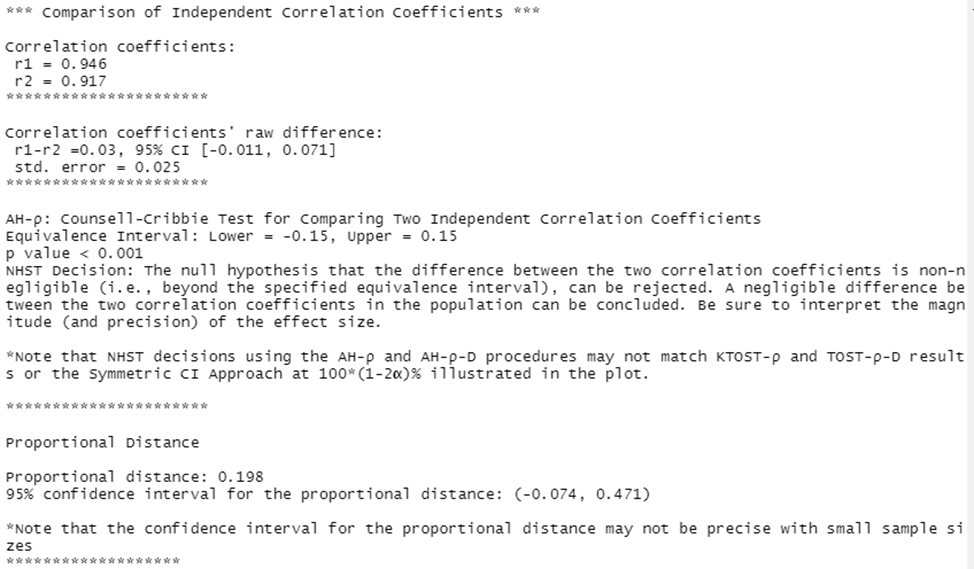
The final output shows the value of the correlation coefficients, the 95% confidence interval of the magnitude of the difference between them, and allows us to conclude that the null hypothesis about the insignificant difference between the two correlation coefficients can be rejected.
8) Test for the insignificance of the difference in mean values in independent groups
Practice: take the CASchools dataframe and test the hypothesis about the equivalence of the average scores in mathematics for students assessed according to different assessment systems
neg.twoindmeans(dv=math,iv=grades,eiL=-1,eiU=1,data=CASchools)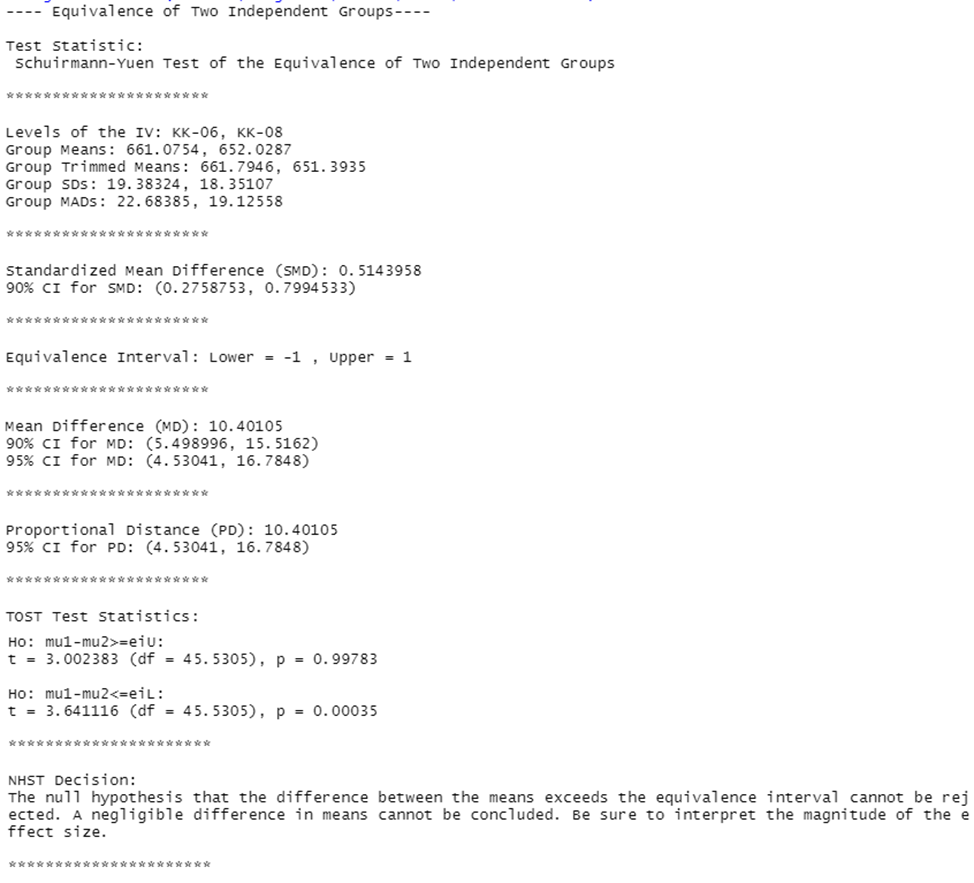
The final output shows the values of the group means, the standardized value of the difference in the means and its 90% confidence interval, and the results of testing two statistical hypotheses that the difference in the means is greater modulo the given extreme values, according to which the null hypothesis cannot be rejected that the difference between the means exceeds the equivalence interval.





