Top 3 Statistical Paradoxes in Data Science
Translation prepared as part of the course “Machine Learning. Professional“.
We also invite everyone to take part in the two-day online intensive Deploy ML model: from dirty code in a laptop to a working service.
Observation errors and subgroup differences cause statistical paradoxes
Observation errors and subgroup differences can easily lead to statistical paradoxes in any data science application. Ignoring these elements can completely discredit the conclusions of our analysis.
Indeed, it is not uncommon to see such astonishing phenomena as subgroup trends that reverse completely in the aggregated data. In this article, we’ll take a look at the top 3 most common statistical paradoxes found in Data Science.
1. Burkson’s paradox
The first striking example is the inverse correlation between the severity of COVID-19 disease and cigarette smoking (see, for example, the European Commission review Wenzel 2020). Cigarette smoking is a well-known risk factor for respiratory disease, so how do you explain this controversy?
Work Griffith 2020, recently published in Nature, suggests that this may be a case of a Collider Bias, also called by the Berkson paradox… To understand this paradox, let us consider the following graphical model, in which we have included a third random variable: hospitalization.
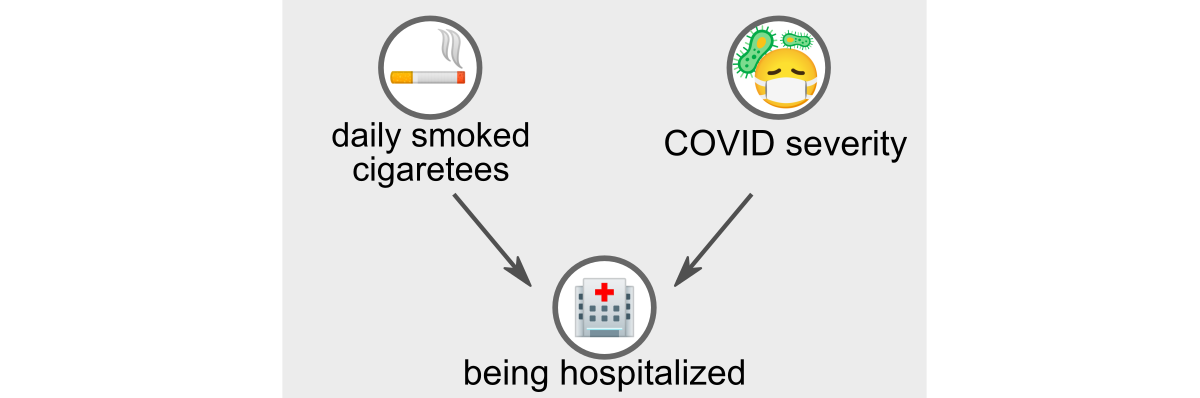
Burkson’s paradox: “hospitalization” is a collider variable for “smoking cigarettes” and for “severity of COVID-19.” (Image by author)
The third variable “hospitalization” is collider the first two. This means that cigarette smoking and severe COVID-19 increase the chances of being hospitalized. The Berkson paradox arises at the moment when we accept the collider as a condition, that is, when we observe the data of only hospitalized people, and not the entire population as a whole.
Let’s take a look at the following example dataset. In the left figure, we have data for the entire population, and in the right figure, we are considering only a subset of hospitalized people (that is, we are using a collider variable).
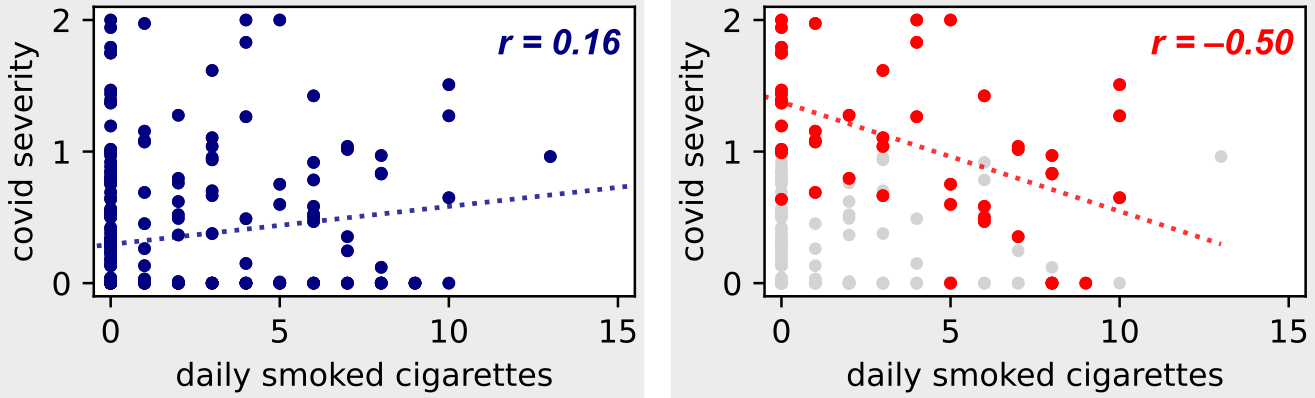
Burkson’s Paradox: If we add a condition according to the hospitalization collider, we see an inverse relationship between smoking and COVID-19! (Image by author)
In the left figure, we can observe the direct correlation between complications from COVID-19 and cigarette smoking, which we expected, since we know that smoking is a risk factor for respiratory diseases.
But in the right figure – where we only look at hospital patients – we see the opposite trend! To understand this, pay attention to the following points.
1) Severe COVID-19 increases the chances of hospitalization. That is, if the severity of the disease is higher than 1, then hospitalization is required.
2. Smoking several cigarettes a day is a major risk factor for various diseases (cardiovascular diseases, cancer, diabetes), which, for whatever reason, increase the likelihood of hospitalization.
3. Thus, if patient mild form of COVID-19, he has more likely to be a smoker! Moreover, unlike COVID-19, the reason for hospitalization will be if the patient has any disease that can be caused by smoking (for example, cardiovascular disease, cancer, diabetes).
This example is very similar to the original work Berkson 1946where the author noticed a negative correlation between cholecystitis and diabetes in hospital patients, although diabetes is a risk factor for cholecystitis.
2. Hidden (latent) variables
Availability hidden variable can also cause the appearance of an inverse correlation between the two variables. While the Burkson paradox arises from the use of the collider condition (which, therefore, should be avoided), this type of paradox can be corrected by assuming a hidden variable as a condition…
Consider, for example, the relationship between the number of firefighters involved in extinguishing a fire and the number of people injured as a result. We expect that an increase in the number of firefighters will improve the result (to some extent – see. brooks law), however, there is a direct correlation in the aggregated data: the more firefighters are involved, the higher the number of injured!
To understand this paradox, consider the following graphical model. The key point is to re-examine the third random variable: “fire severity”.

Latent Variable Paradox: “Fire severity” is a latent variable for “n firefighters involved” and “n injured”. (Image by author)
The third hidden variable correlates directly with the other two. Indeed, more severe fires tend to result in more injuriesand at the same time for extinguishing requires a large number of firefighters…
Let’s take a look at the following example with a dataset. In the left figure, we reflect the general data for all types of fires, and in the right figure, we consider only information corresponding to three fixed degrees of fire severity (i.e., we condition our observational data for a latent variable).
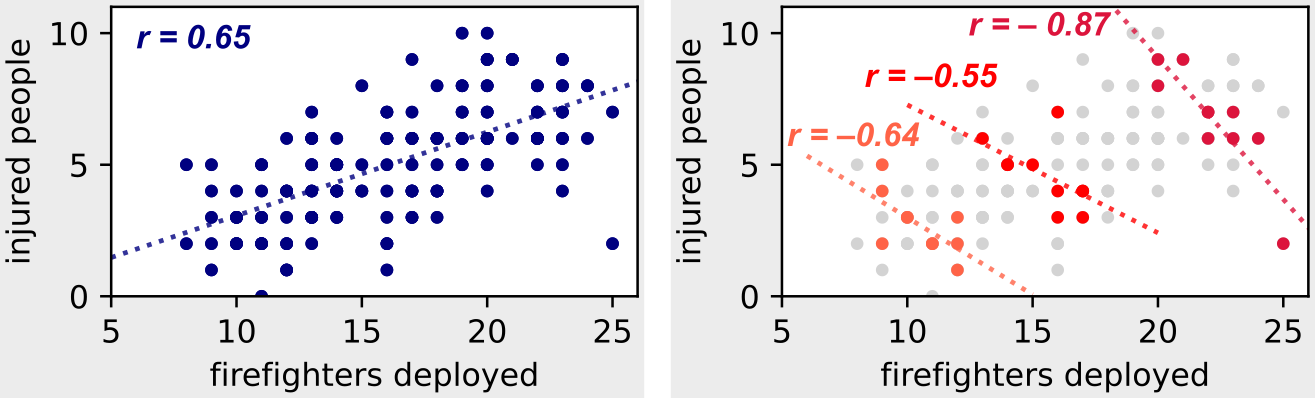
Hidden Variables: If we take the hidden variable “fire severity” as a condition, we see an inverse correlation between the number of firefighters involved and the number of injured! (Image by author)
In the right picture, where are we we take as the condition for observation data the severity of the fire, we see the inverse correlation we expected.
For a given severity of the fire, we actually see that the more firefighters are involved, the fewer people are injured…
If we look at high severity fireswe will see that same trendeven though the number of firefighters involved and the number of injuries are increasing.
3. The Simpson paradox
Simpson’s paradox – this is an amazing phenomenon when we constantly observe some kind of tendency arising in subgroups, and which changes to the opposite, if these subgroups are combined. This is often due to imbalance of classes in data subgroups…
A sensational case of this paradox occurred in 1975, when Bickel University of California enrollment rates were analyzed to find evidence of gender discrimination, and two clearly contradictory facts were revealed.
One side, he noticed that on each faculty number of accepted female applicants are higher than male applicants…
On the other hand, total acceptance rate among of female applicants was lower than that of male applicants…
To understand how this could be, let’s consider the following dataset with two faculties: Faculty A and Faculty B.
Out of 100 male applicants: 80 applied for Faculty A, of which 68 were accepted (85%), and 20 applied for Faculty B, of which 12 were accepted (60%).
Out of 100 female applicants: 30 applied for Faculty A, of which 28 were accepted (93%), while 70 applied for Faculty B, of which 46 were accepted (66%).

Simpson’s Paradox: Female applicants are more likely to be accepted in every faculty, but overall admission rates for females are lower compared to males! (Image by author)
The paradox is expressed by the following inequalities.

Simpson’s Paradox: Inequality at the heart of an apparent contradiction. (Image by author)
We can now understand the origin of our seemingly conflicting observations. The point is that there is a tangible class gender imbalance among applicants in each of the two faculties (Faculty A: 80–30, Faculty B: 20–70). Really, most female students applied for a more competitive Faculty B (which has low reception rates), while most male students applied for the less competitive Faculty A (which has higher acceptance rates). This leads to the conflicting data that we received.
Conclusion
Hidden variables, collider variables, and class imbalance can easily lead to statistical paradoxes in many practical points of data science. Therefore, these key points need to be given special attention in order to correctly identify trends and analyze the results.
Learn more about the course “Machine Learning. Professional“
Participate in an online intensive “Deploy ML model: from dirty code in a laptop to a working service”





