The horse moves on bits. Chess Bitboard
A chess horse stands on a chessboard and looks thoughtfully into the chessboard.
How many different moves can he make?

Praise to the inventor of chess, on the board 64 cells.
Praise to the computer architect – at type ulong also 64 bit.
This coincidence had to happen!
The brilliant idea suggests itself – to store whole board in one whole! There is even a special term for this decision – Bitboard – bit board.
So how fast find the number of moves a chess horse using this idea?
Given: knightNr – the cell number of the board where the horse is (from 0 to 63).
It is necessary: movesCount – the number of fields where he can go (from 2 to 8).
Algorithm.
1. Convert the horse’s cage number to ulongbit value
knightNr -> knightBits
2. Set bits for all possible moves of the horse
knightBits -> movesBits
3.Count the number of unit bits
movesBits -> movesCount
The first step is very simple, you need to shift the zero bit to the left by the specified number of positions.
ulong knightBits = 1 << knightNr;The second step is a bit more complicated. A horse can go in 8 different directions. We will consider these offsets not “horizontally / vertically”, but by bit positions. That is, we consider how many positions you need to shift the start bit for each move. Then we “add up” everything with a logical “or” operation.
Let's start listing the moves from the left side of the board to the right:
movesBits = knightBits << 6 | knightBits >> 10 // on b5 and b3
| | | knightBits << 15 | knightBits >> 17 // on c6 and c2
| | | knightBits << 17 | knightBits >> 15 // on e6 and e2
| | | knightBits << 10 | knightBits >> 6 // on f5 and f3;
True, cool !?
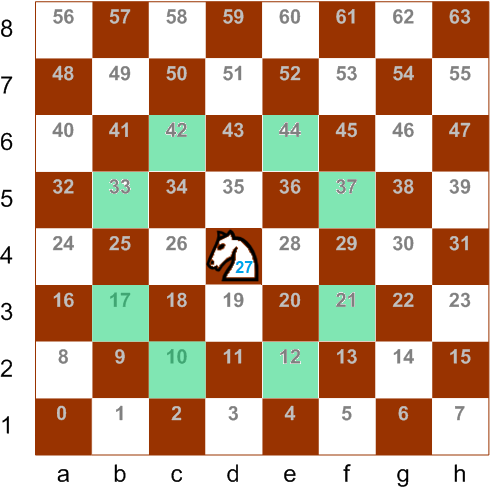
Unfortunately, there are “black holes” at the edges of the board. For example, according to this algorithm, from cell a4 (bit # 24) you can get to cell g2 (bit # 14 = 24 – 10), this jump is teleportation spherical chess horse in vacuum on the board through black hole extreme verticals…
To exclude the quantum jump of the horse over the edge of the board, it is necessary to “disconnect” the extreme bands after moving. For example, for moves +6 and -10 (two cells to the left), it is necessary to cancel the obtained values on the g and h verticals, since you cannot end up on these verticals after moving “left” for two moves.
To do this, we need 4 bit grid constants, in which all bits are set to 1, except for the indicated verticals. Namely:
ulong nA = 0xFeFeFeFeFeFeFeFe;
ulong nAB = 0xFcFcFcFcFcFcFcFc;
ulong nH = 0x7f7f7f7f7f7f7f7f;
ulong nGH = 0x3f3f3f3f3f3f3f3f;
At the top and bottom of the chessboard there are also “black holes” that completely absorb the horse, so they do not need to be checked separately.
Now the algorithm for generating permissible horse moves looks like this:
movesBits = nGH & (knightBits << 6 | knightBits >> 10)
| | | nH & (knightBits << 15 | knightBits >> 17)
| | | nA & (knightBits << 17 | knightBits >> 15)
| | | nAB & (knightBits << 10 | knightBits >> 6);
It works very (!) Fast.
A few ticks – and we have a bitmap of all possible horse adventures. The most amazing thing is that this algorithm works fine even if there are several horses on the board. He at once generates all the possible moves for all the horses! True, great !?
It remains to count the number of bits
The easiest way – shift the number by 1 bit to the right and count the ones. Difficulty – 64 operations. Memory – 64 bits.
Fastest way – create a cache / array with 65536 elements, in which the number of bits for each index is written from 0 to 65535. And add 4 elements from this array that correspond to the next 16-bit segments of the number.
Difficulty – 4 operations. Memory – 64 kilobytes.
But we will consider the trickiest waywhose complexity is equal to the number of unit bits in the number. Since there are not many moves, this approach will be the most optimal for us.
To begin with, we note that subtracting a unit from a number, we turn all the “right” zeros into units, and the outermost unit into zero:
1001010100010000 - 1 =
1001010100001111
Next, apply the logical and operation for these numbers:
1001010100010000 &
1001010100001111 =
1001010100000000
As you can see, in such a tricky way, we reset the rightmost unit to zero. Repeat this operation until we get zero as a result. How many iterations, so many single bits. True, great !?
This is how this algorithm is written in full:
int movesCount = 0;
while (movesBits! = 0)
{
movesBits & = (movesBits - 1);
movesCount ++;
}
The problem is solved!
This task has another, very simple, purely logical solution: to determine the distance of the knight from the edge of the chessboard (in the corner there are 2 moves, near the edge from 3 to 6 moves, in the center of 8 moves). But if we were to solve the problem “head on” in this way, we would not know about the bit board, about vertical bit masks, about the algorithm for quickly counting single bits and about black holes for spherical horses in a vacuum …
Now we know all about it. The life of a chess programmer has become richer and more meaningful, cheers!
Independent task: do the same for the Chess King.





