Spatial Transformer Networks in MATLAB
This article will raise the topic of building custom layers of neural networks, using automatic differentiation and working with standard deep learning layers of neural networks in MATLAB based on a classifier using a spatial transformation network.
The Spatial Transformer Network (STN) is one example of differentiable LEGO modules that you can use to build and improve your neural network. STN, applying a trainable affine transform with subsequent interpolation, deprives images of spatial invariance. Roughly speaking, the task of STN is to rotate or reduce / enlarge the original image so that the main classifier network can more easily identify the desired object. An STN block can be placed in a Convolutional Neural Network (CNN), working in it for the most part independently, learning on gradients coming from the main network (for more details on this topic, see the links: Habr and Manual).
In our case, the task is to classify 99 classes of car windshields, but first, let’s start with something simpler. In order to get acquainted with this topic, we will take the MNIST database from handwritten numbers and build a network of MATLAB deep learning neural layers and a custom affine image transformation layer (you can see the list of all available layers and their functionality by link).
To implement a custom transformation layer, we will use a custom layer template and MATLAB’s ability to automatically differentiate and build back propagation of the derivative of the error, which is implemented through deep learning arrays for custom training cycles – dlarray (you can familiarize yourself with the template by link , you can familiarize yourself with dlarray structures by link).
In order to implement the capabilities of dlarray, we need to manually register the affine transformation of the image, since MATLAB functions that implement this feature do not support dlarray structures. The following is the transformation function we wrote, the entire project is available by link…

Since the affine transformation is reversible, the easiest way to check that a function is working correctly is to apply the transformation to the image, then find the inverse matrix and re-transform it. As we can see in the image below, our algorithm is working correctly. On the left we have input images, on the right we have output images, above – above the right images – a transformation superimposed on the image is signed.

It is also important to clarify what specific changes are superimposed on the images by different numbers of the transformation matrix. The first line imposes transformations along the Y axis, and the second along the X. The parameters perform resizing (zoom in, zoom out), rotation and shift of the image. The transformation matrix is described in more detail in the table.
Y | The size | Turn | Bias |
X | Turn | The size | Bias |
Now that we have figured out the theoretical component, let’s move on to implementing the network using STN. The figures below show the structure of the constructed network and the training results for the MNIST database.


Based on the learning outcomes, namely how the network transforms the image and what percentage of guessing it demonstrates, we can conclude that this version of the network is fully functional.
Now that we have received a decent result on the MNIST database, we can move on to the windshields we have.
The first difference between the inputs is that the numbers are grayscale images and the glasses are RGB images, so we need to change the transform layer by adding a loop. We will apply a separate transformation to each of the image layers. Also, to simplify training, add weights to the transformation layer by which we will multiply the transformation matrix, and set these weights to 2, with the exception of the image shift weights, set them to 0, so that the network learns, first of all, to rotate and change image scale. Also, if we take less data, then the network will take longer to rebuild the STN weights in search of useful information, since useful information is located at the edges of the image, and not in the center, unlike a network with numbers. Next, we need to replace part of the classifier, as it is too weak for our input. In order not to change the structure of the STN itself, we will bring the image to a form similar to numbers, adding a layer of normalization and a dropout to reduce the amount of input data in the STN.
Comparing the data at the input of the network with numbers and glasses, you can see that on the glasses the range of values varies from [0;255], and in numbers from [0;1]and also in numbers, most of the matrix is zeros. Examples of input data are shown below.

Based on the above data, normalization will be performed according to the principle of dividing the input data by 255 and zeroing all values less than 0.3 and greater than 0.75, as well as from the three-dimensional image, we will leave only one dimension. The image below shows what is being fed in and what remains after the normalization layer.

Also, due to the fact that we do not have a lot of data for testing and training the network, we will artificially increase their volume due to affine transformation, namely, rotating the image by a random degree within [-10;10] and adding a random number to the image matrix to change the color palette within [-50; 50]… In the read function, we will use the standard MATLAB functions, since we do not need to operate on dlarray structures in it. Below is the function used to read input images.
Below is the structure of the network with the changes made and the results of training this network.

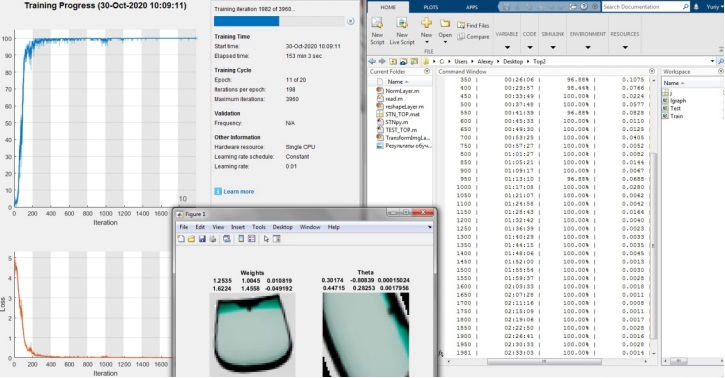
As we can see, the network highlighted useful features, namely the central part of the image, due to this, by the end of the first epoch, it reached a guessing percentage above 90. Since the edges of the images are the same, the network learned to classify excellent features, and, due to this, it enlarges the central part, bringing the left and right edges out of the border of the image supplied to the classifier. At the same time, the network rotates all images so that they do not differ in the angle of inclination, due to which the classifier does not need to adjust the weights for different angles of image inclination, thereby increasing the classification accuracy.
For comparison, let’s take and test a network without using STN, leaving only the classifier we have. Below are the learning outcomes of this network.

As we can see, the network really learns more slowly and achieves lower accuracy for the same number of iterations.
Summing up, we can conclude that STN technology is relevant in modern neural networks and can increase the learning rate and the accuracy of network classification.




