How to explain binary notation
Quite quickly, you will find that it is not so easy to explain how the binary count works.
It’s obvious to you that after 11 it’s 100, and for a beginner it may not be clear for a long time.
So, to increase the speed of understanding, we decided to make didactic material.
Problem
It’s important to note that even the Harvard University computer science CS50 course doesn’t help.

A guy from an American university simply states that “zero is zero,” “one is one,” and then goes 10, and then 11. Understood? I think no. So ask someone who is not a programmer, but what will be the next number – it is highly likely that he will not be able to answer. Too quickly slipped the idea of transferring the discharge.
The same applies to school translation methods: firstly, these methods are academically dry, and secondly, they are not intuitive – for example, it is not obvious why, after cascading by 2, you need to put the bits backwards.

And if it is not clear, then it is not interesting. And if there is no interest, then it is difficult to remember.
We took all this into account, and decided to make an interesting and gradual explanation.
What do we offer
First you need to explain how the ordinary decimal number system works – both about the final “alphabet” of numbers and about the idea of transferring the category. This is how the understanding of the principle of “number system” develops.
Only then can we move on to the idea of a binary system – and now the student is slowly, but quite confidently, saying “1, 10, 11, 100”.
Further, we decided to try a completely non-school method – an explanation of the binary count on the fingers: this is when the bent finger is 0, and the extended one is 1.
I tested it on teenagers: you show them: “this is 1, this is 2, this is 3 – now show me 4”. And the whole class is concentrated, slowly showing middle fingers. Excellence in eschatological enthusiasm, the rear desks poke each other in the face and shout “four on you!”.
Provocatively? Yes. Memorized? 100%.
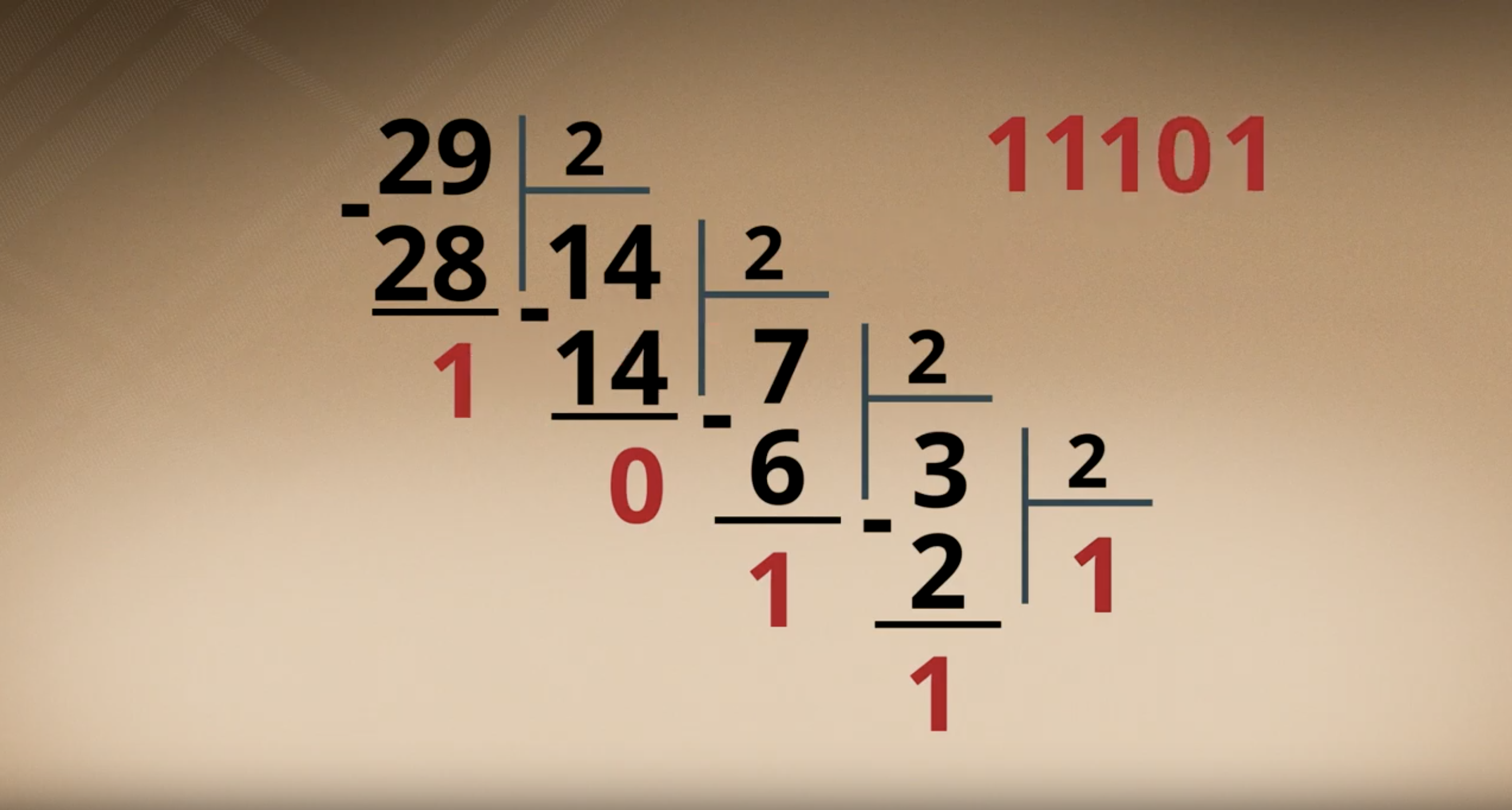
Now that the topic has become “ours,” we can move on to the topic of translating numbers from one number system to another — it’s better to start with the classic school dry translation (to be honest, more to string down).
And only then, with the help of animation, explain the idea of translation right on the fingers, and then again on the fingers count the number 132 into the middle fingers already on both hands.
For dessert, we show where the binary and hexadecimal systems are used in real life.
The binary system is for example the QR codes around us.
A hexadecimal system is basically CSS color codes and hashes of different styles, from MD5 to UUID.
So, here is the whole package of video lessons (they are free, on YouTube):
- Binary number system
- Translation from 2 to 10 number system
- Translation from 10 to 2 number system
- The application of the binary number system in real life
- Hexadecimal notation
- The application of the hexadecimal number system in life
- Using the octal number system – file permissions
We hope this material will be useful to you in the difficult task of teaching programming.