Burnside’s lemma. Poya’s theorem

Let there be a set x.

Definition. Group G operates on many x, if \forall g \in Gand \forall x \in Xelement action defined g per element x (denoted gx), having the following properties:

  1. gx\inX;

  2. \forall {g}_{1}, {g}_{2} \in G, \forall x \in Xdone ({g}_{1}{g}_{2})x = {g}_{1} ({g}_{2}x);

  3. \forall x \in Xdone ex = x.

Example 1 X = \mathbb {R}^{2}, G = \{ \mathbb{R} \setminus \{ 0 \}, \cdot \}.

For elements (x,y)\in X:g(x,y) = (gx, gy),where g– action, (gx,gy) \in \mathbb{R}{^2}.

Example 2. Action composition z = sin(ln(x)).

Action composition
Action composition

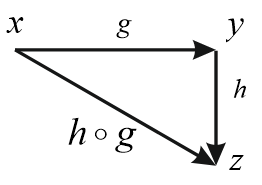
Example 3 Vector rotation (x,y)on the corner \alpha counterclock-wise [0, 2\pi), + \text{ mod} 2\pi \}.” alt=”G = \{ [0, 2\pi), + \text{ mod} 2\pi \}.” src=”https://habrastorage.org/getpro/habr/upload_files/c48/928/ce5/c48928ce5827260038895b32fc3b7377.svg” width=”203″ height=”22″/>

Пример 4. X = \mathbb{B}^{n}(упорядоченные наборы из нулей и единиц длиной n).

Группа перестановок G = {S}_{n}с операцией композиции.

p = ({p}_{1}, {p}_{2}, \ldots, {p}_{n}) \in {S}_{n}.

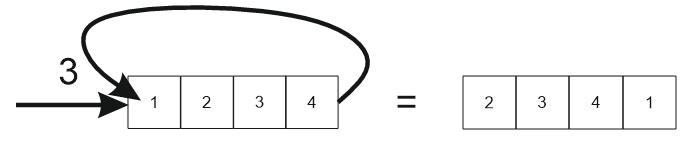
Пример 5. ПустьX = {T}^{n}(упорядоченные числовые наборы – массивы чисел), группа циклических сдвиговG = \{ \{ 0, \ldots, n-1 \}, + \text{ } mod \text{ } n \}.

Обратный элемент к элементу a \in G вычисляется следующим образом: {a}^{-1} = (n-a) \text{ } mod \text{ } n.

Циклический сдвиг массива на 3 позиции вправо
Циклический сдвиг массива на 3 позиции вправо

Классы эквивалентности (орбиты)

Определение. Пусть группа Gдействует на множество X.Тогда орбитой элемента x \in Xназывается множество: Orb(x)=\{y∈X∣∃g∈G:g⋅x=y\}.Множество всех орбит обозначается так:X/G.

Пример 1. Множество X– числовые массивы длиной n. G– группа перестановок длины n.X = {T}^{n},G ={S}_{n}.

В данной перестановке существует единственный класс эквивалентности.
В данной перестановке существует единственный класс эквивалентности.

Пример 2. {T}^{n}: \{ 0, \ldots, n-1 \} + \text{ } mod(n)циклический сдвиг массива длиной n.

Пример 3. X = {A}^{k}_{n}– размещения из nпо k.G = {S}_{n}– перестановки nэлементов. Классами эквивалентности в данном случае будут сочетания из nпо k:X / G = {C}^{k}_{n}.

Пример 4. Группа поворотовG = \{ \alpha \in [0, 2\pi]+ \text{ } mod (2\pi )\}affects manyX = {\mathbb{R}}^{2}. Orbits (equivalence classes) in this case are concentric circles.

Orbits
Orbits

fixed point

Definition. Let the group Gaffects many x.fixed point for element gsuch an element is called x,for which gx = x.

Definition. Let a finite group Goperates on many x.For element x ∈ Xits stabilizers (in the group G) is a subset of elements of the group Gleaving it (element x) in place.

Example 1 Multiplication of coordinates of a point in a plane \mathbb{{R}^{2}}to a constant.

g(x,y) = (gx, gy), x \in \mathbb{R}, y \in \mathbb{R}, (x,y) \in \mathbb{R}^{2}, (gx , gy) \in \mathbb{R}^2.

If g = 1,then \forall (x,y) \in \mathbb{R}^2performed (x, y) = (gx, gy).

If g\ne 1,then \exists! (x, y): (x, y) = (gx, gy).And this point (0.0).

\begin{equation*}\begin{cases} {St}_{g} = \{(0,0)\}, & g \ne 1; \\ {St}_{g} = {\mathbb{R}}^{2}, & g = 1. \end{cases} \end{equation*}

Example 2 Consider an array consisting of 5 numbers and some permutation to it:

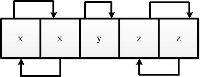
How to find the number of fixed points in an arbitrary permutation?

The permutation is divided into cycles.

In each cycle, the elements must be equal (the same).

Between cycles, elements can be correlated arbitrarily. The number of cycles is gcd(n,d).

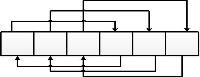
n = 6, d = 3. gcd(6,3) = 3.
n = 6, d = 3. gcd(6,3) = 3.
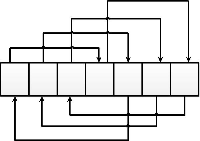
n = 7, d = 3. gcd(7,3) = 1.
n = 7, d = 3. gcd(7,3) = 1.

Burnside lemma

Theorem. The number of orbits is equal to the average power of the stabilizer of the elements of the group G.

X/G = \frac{\sum_{g \in g} |{St}_{g}|}{G}.

Example. T = \mathbb{B}, n = 3.

000

001

010

one hundred

110

101

011

111

123

000

001

010

one hundred

110

101

011

111

132

000

010

001

one hundred

101

110

011

111

213

000

010

one hundred

010

110

011

101

111

312

000

one hundred

001

010

011

110

101

111

231

000

010

one hundred

001

011

011

110

111

321

000

one hundred

010

001

011

101

110

111

\widetilde {X}

{x}_{1}

{x}_{2}

{x}_{3}

...

{x}_{i}

\ldots

{x}_{k}

{g}_{1}

{g}_{2}

{g}_{3}

\ldots

{g}_{j}

{g}_{j}{x}_{i}

\ldots

{g}_{n}

|G| \cdot |X / G| = \sum_{x \in X} |Stx| = \sum_{x \in X} \sum_{g \in G} [ gx = x ] = = \sum_{g \in G} \sum_{x \in X} [gx = x] = \sum_{g \in G} |{I}_{g}|.|X / G| = \frac{\sum_{g \in G} |{I}_{g}|}{|G|}.

Example. Consider a set of binary arrays of length 3. n = 3, X = {\mathbb{B}}^{3}.

Group G = {S}_{3}affects many X = {\mathbb{B}}^{3}.

Let us calculate the average power of the stabilizer of the elements of the group G.

\pi

|{I}_{\pi}|

123

8

132

four

213

four

231

2

312

2

321

four

\frac{8+4+4+2+2+4}{6} = 4.

By the Burnside lemma, the number of orbits (equivalence classes) is 4.

Poya’s theorem

Polya’s theorem is a generalization of Burnside’s lemma. It also allows you to find the number of equivalence classes, but already using a value such as number of cycles per permutation.

Let the number of cycles in the permutation gequals C(g).

The number of colors for coloring the beads is k.

The number of cycles is С(g) = GCD(n,d).

Each cycle can be colored in one of kcolors: {k}^{gcd(n,k)}.

For all cyclic shifts: \sum_{d=0}^{n-1}.

The number of possible cyclic shifts is n.

The number of necklaces can be calculated using the formula:

\frac{\sum_{d = 0}^{n-1} {k}^{gcd(n,d)}} {n}.

Example. k=3, n=5.

Calculate the number of necklaces using the Poya theorem:

d = 0: gcd(0.5) = 5,d = 1: gcd(1, 5) = 1,d = 2: gcd(2, 5) = 1,d = 3: gcd(3, 5) = 1,d = 4: gcd(4, 5) = 1.\frac{3^5 + 3 + 3 + 3 + 3}{5} = \frac{255}{5} = 51.

We obtain a similar result by the Burnside lemma:

|{St}_{0}| = 3^5, |{St}_{1}| = 3, |{St}_{2}| = 3, |{St}_{3}| = 3, |{St}_{4}| = 3. \frac{3^5 + 3 + 3 + 3 + 3}{5} = \frac{255}{5} = 51.