Log-Sum-Exp Trick: How Function Properties Make Classifiers Work Real

In this article, we will look at what a classifier is, talk about multiclass classification using neural networks. Then, having familiarized ourselves with the context, let’s move on to the main topic of the post – to the Log-Sum-Exp Trick. Let’s write the formulas and see how this trick can help avoid floating point overflows.
Logistic regression
In classical machine learning, there is a classification method called logistic regression… A logistic regression classifier is usually designed to separate data into two classes. For example, an email classifier might return a value of 0.9, which could mean 90% chance that the message is spam, and 10% is not spam. In this case, the sum of the probabilities always gives one. Logistic regression gives such probabilities based on the output sigmoid function…
The following questions arise here. What if our data needs to be divided into more than two classes? What function should be used so that the outputs of the classifier can be interpreted as probabilities?
Multiclass neural networks
As a classifier that produces several probabilities at once, let’s consider a neural network. Such neural networks make predictions using the function softmax…
In the formula above – output values of the neural network for each class,
– Probabilities converted using softmax.
Softmax generalizes the problem of obtaining probabilities when the classifier has more than two outputs.
For example, if we trained the classifier on images to determine what is shown in the picture, then we can see something similar to the following:
this is how the application of the softmax to the outputs of the neural network is schematically depicted,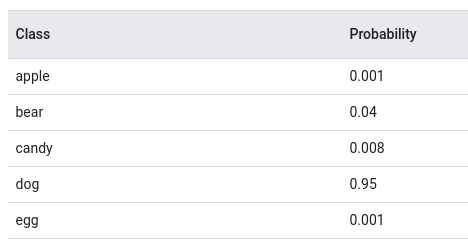
and this is how the probability distribution will look like, they add up to one (a source).
Overflow problem when calculating Softmax
Logits coming from the neural network can take arbitrary values on the real line. Consider what happens if in Python we try to calculate the softmax for the third component of a given vector:
import numpy as np
x = np.array([-100, 1000, -100, 5, 10, 0.001])
exp_x = np.exp(x)
print("Возведение в степень X: ", "n", exp_x)
print("Сумма экспонент: ", "n", np.sum(exp_x))
print("Третья вероятность: ", np.exp(x[3]) / np.sum(exp_x))
Output:
Возведение в степень X:
[3.72007598e-44 inf 3.72007598e-44 1.48413159e+02
2.20264658e+04 1.00100050e+00]
Сумма экспонент: inf
Третья вероятность: 0.0
We see that the value 1000 leads to overflow and this ruins all further normalization.
Log-Sum-Exp
To solve the problem posed above, it is proposed to use the function
– Log-Sum-Exp function.
Its definition follows from the name – it is a sequential application to the input argument: exponent, summation and logarithm. You can often see that this function is called the differentiable analogue of the maximum function of several variables. Differentiability is an extremely useful property for finding extrema.
 (a source)
(a source)
As you can see in the picture above, lse (x) is smooth everywhere, unlike max (x) function.
Log-Sum-Exp Option without Overflow
If we try to calculate the LSE function of the vector x, then we will also encounter an overflow problem, since the sum involves exponents of an arbitrary, possibly large, degree. The overflow problem can be eliminated by transformations based on the properties of the function.
Let the execution result has the meaning
, then we can write the following equation:
Apply the exponent to both sides of the equation:
Stunt time. Let be then we take out from each term
:
Now let’s test the new formula in practice:
import numpy as np
x = np.array([11, 12, -1000, 5, 10, 0.001])
y = np.array([-1000, 1000, -1000, 5, 10, 0.001])
def LSE_initial(x):
return np.log(np.sum(np.exp(x)))
def LSE_modified(x):
c = np.max(x)
return c + np.log(np.sum(np.exp(x - c)))
# с экспонентами, не приводящими к переполнению
print('Исходная LSE(x): ', LSE_initial(x))
print('Преобразованная LSE(x): ', LSE_modified(x))
# с экспонентой в 1000й степени
print('Исходная LSE(y): ', LSE_initial(y))
print('Преобразованная LSE(y): ', LSE_modified(y))Output:
Исходная LSE(x): 12.408216490736713
Преобразованная LSE(x): 12.408216490736713
Исходная LSE(y): inf
Преобразованная LSE(y): 1000.0It can be seen that even in the case when one of the terms turns into float inf, the modified version of lse (x) gives the correct result.
Log-Sum-Exp Trick
Now let’s go directly to the trick. Our original task is to compute the softmax for a set of real values without getting incorrect results due to overflow.
To achieve this, let’s convert the softmax function to a form that depends on …
Let be in the softmax formula is
, then our equality will take the following form:
Let’s apply a number of transformations:
It turns out that instead of calculating the original example, you can calculate the following:
Let’s apply the new formula for calculating the softmax:
import numpy as np
x = np.array([11, 12, -1000, 5, 10, 0.001])
y = np.array([-1000, 1000, -1000, 5, 10, 0.001])
def softmax_initial(x):
return np.exp(x) / np.sum(np.exp(x))
def LSE(x):
c = np.max(x)
return c + np.log(np.sum(np.exp(x - c)))
def softmax_modified(x):
return np.exp(x - LSE(x))
# с экспонентами, не приводящими к переполнению
print('Исходный Softmax(x): ', softmax_initial(x))
print('Преобразованный Softmax(x): ', softmax_modified(x))
print('Суммы вероятностей: {} {}n'.format(np.sum(softmax_initial(x)), np.sum(softmax_modified(x))))
# с экспонентой в 1000й степени
print('Исходный Softmax(y): ', softmax_initial(y))
print('Преобразованный Softmax(y): ', softmax_modified(y))
print('Суммы вероятностей: {} {}'.format(np.sum(softmax_initial(y)), np.sum(softmax_modified(y))))Output:
Исходный Softmax(x): [2.44579103e-01 6.64834933e-01 0.00000000e+00 6.06250985e-04
8.99756239e-02 4.08897394e-06]
Преобразованный Softmax(x): [2.44579103e-01 6.64834933e-01 0.00000000e+00 6.06250985e-04
8.99756239e-02 4.08897394e-06]
Суммы вероятностей: 0.9999999999999999 1.0000000000000004
Исходный Softmax(y): [ 0. nan 0. 0. 0. 0.]
Преобразованный Softmax(y): [0. 1. 0. 0. 0. 0.]
Суммы вероятностей: nan 1.0Here, similar to the results with the transformed lse (x), you can see that the modified version of the softmax is more stable and does not suffer from overflow in the calculation. The sum of the probabilities obtained from softmax gives one, for all examples of vectors. This behavior is expected from this function.
Conclusion
In this post, we took a look at several commonly used functions in machine learning. Discussed superficially how a multiple classifier based on a neural network works. And most importantly, we figured out how to avoid incorrect results when it is necessary to display the probabilities of attribution to a certain class for such a neural network.
The article was prepared as part of the course “Mathematics for Data Science”… I also invite everyone to watch the recording of a free demo lesson about linear spaces and displays.





