Eight colors of the rainbow: about color in terms of mathematics
For more than five years we have been publishing articles on various topics of computer vision on Habré. Most often they are associated with document recognition, because we are always very eager to share with you everything cool and new that we did in Smart IDReader. Although we honestly try to present our knowledge in a “universal” manner so that you, our Habr readers, can easily use them in your projects and startups. Today we decided to go further and present to a wide audience a fundamental mathematically harmonious material on the theme of color, outlined in simple words.
Color definition
Schrodinger’s definition can be considered one of the most successful definitions of color: color is a common property of light of different spectral composition to cause the same visual sensation. Important in this definition is the understanding of color not as some absolute property of light, but as a phenomenon depending on the observer: if two rays of light cause the observer the same sensations, then the color is the same, and otherwise it is different.
However, this definition cannot be called completely successful. After all, it can be used only in colorimetric conditions, that is, specially designed so that a person can act as a measuring device. For example, you look into the eyepiece, and your eyes are evenly illuminated with the light of some spectral composition. In all the more difficult situations, for example, when you just look around and see a red shirt or a green meadow, it turns out that it is not possible to simply study the sensations of the observer and build on this basis color theory.
We know from the course of physics thanks to Newton that in the white light there is a rainbow. It is manifested by the dispersion of refraction of light in a prism or suspension, which occurs in the air during mushroom rain. This happens as follows: a prism directs light of different wavelengths in different directions, and we see almost monochromatic (i.e., a single wavelength) radiation in each direction. Going through different directions, we see light of different wavelengths, which makes us feel like a transition from violet through blue, yellow and then to red. Each of the colors of the rainbow directly corresponds to a specific wavelength, but this does not mean that individual wavelengths can be attributed to all colors in general.
How the sensor works
Since the color depends on the perception of the observer, let’s figure out what is sensor. A sensor is the organ that supplies the observer with comprehensive visual information. For humans, this is the eye, and for the robot, an RGB camera. The color sensor is characterized by a set of photosensitive elements of various types. In the eye, in bright light conditions, three types of cones are active: “blue”, “red” and “green”, each of which has its own spectral sensitivity. Spectral sensitivity is a function of the magnitude of the response to one quantum, that is, to one portion of light of a certain wavelength. For example, the “blue” cone is most sensitive to wavelengths in the region of 450 nanometers. We can assume that when radiation of any spectrum falls on a small area of the retina of the eye, there are three signals from this area of the retina, three non-negative values that show how much the “blue”, “red” and “green” cones were excited on this site on average. Thus, the human retina or the photosensitive matrix of the camera projects the spectral signal into three-dimensional color spacesabout, the coordinates in which are indicated , and . The origin (“zero”) in it will be the absence of radiation – a situation where none of the three types of receptors is excited.
Color
The distance from zero in the color space is called brightnessis a power feature. If we take a light source and increase its power, the corresponding point in the RGB color space will move away from zero in a straight line through the origin. The main diagonal, that is, those values of triples in which the color components are equal – this achromatic axis, on it lie gray colors.
For further analysis, we’ll remove the brightness from the color. To do this, centrally project (with the center of projection at zero) the entire color space on any plane that does not pass through zero. All points in the color space that differ only in brightness are projected onto the same point on the plane. We’ll get color plane, and we call a pair of coordinates on this plane color, that is, that part of the color that is not related to the radiation power.
How many colors are there in the rainbow?
Let us now consider all kinds of colors perceived by the human eye and ask ourselves: what will this set look like if we project it onto the color plane?
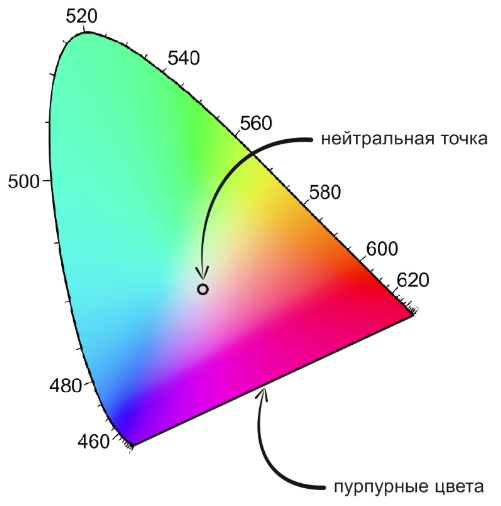
To do this, first run through all the wavelengths of the visible spectrum (from 380 to 700 nanometers) and draw the corresponding points (pure spectral colors) to the color plane. We get a curved curve (see the figure at the very beginning of the article), called spectral locus.
It will be interesting for mathematicians to note that in RGB space the spectral locus is a closed drop-shaped curve with a single kink at the origin, which, when centrally projected with a center at the same origin, turns into an open curve on the color plane.
Since the sensor provides a linear projection of all kinds of spectra in the visible range into the color space, any achievable combinations (R, G, B) can be obtained as a convex combination (“mixture”) of those reactions that are generated by pure colors. This also applies to projections on the color plane. Thus, physically achievable colors lying in convex hull spectral locus. And, since the spectral locus of a person does not have concavities, it is supplemented to a convex hull with one single segment connecting its ends. The resulting figure is usually called color trianglealthough, as we see, the angle at this “triangle” is actually only two, and instead of the third there is a rounding in the region of 520 nanometers. So, the colors of all the colors visible to a person make up a color triangle – a convex curvilinear figure with two vertices.
We now consider the intersection point of the achromatic axis in RGB space with the color plane. This point will be called neutral and match white. Each direction from the neutral point to the border of the color triangle defines Color tone. The color of the dot on the border is called saturated the color of a given tone, and all points between neutral and saturated can be obtained as a mixture of this saturated color with white in different proportions.
As can be seen from the figure, most saturated colors are pure spectral colors, that is, points of the spectral locus corresponding to the monochrome radiation of different colors of the rainbow from 380 to 700 nanometers. However, on a straight line segment of the border of the color triangle from 700 to 380 nanometers, we see saturated colors, which do not correspond to any pure color of the spectrum. These are magenta colors called non-spectral. Purple flowers cannot be associated with any single wavelength, but they can be obtained as a sensor response to a mixture of red and violet waves.
Is it possible to see the purple color in the rainbow? We have already figured out that in a single rainbow it is not. But sometimes in the sky double rainbows of various nature can be seen. Among them is a reflected rainbow above the surface of the water with very low sun. In such a rainbow, after the violet color again goes red, orange and so on. And at the junction of red and purple, you can see their mixture – purple. It turns out that there can be eight colors in the reflected rainbow!
How to see non-existent colors
For those who closely followed the reasoning, the question may arise: what about the part of the color plane that is outside the color triangle? These points can even have quite positive coordinates. . Are these the colors? Can a person see a color that is not caused by any spectral radiation falling into his eye? Hard to say, but maybe yes. For example, when a brick falls on his head and “birds” and “stars” appear, it is likely that some of the colors he sees are physically unattainable. This is because at the moment of mechanical action on the neurons of the brain, the signals in them are quite random in nature, and at the same time, such a combination of signals can occur that never arises as a result of the effect of radiation on the human eye. Similarly, we can assume that a person can see non-existent colors in a dream.
Standard observer
As noted above, the color space depends on the observer. If the sensors of two observers give different responses to radiation of the same spectrum, then the color spaces they constructed (and also the color triangles) will turn out different. Therefore, for numerical experiments, standard observerwhose receptor sensitivity curves are thought to well model human biochemistry and perception.
Also, for a standard observer, the sensitivity curves are normalized so that if all three types of photosensitive elements are excited by a source that has the same spectral brightness for each of the wavelengths, then , and Sensor reactions will be equal to each other. This means that white daylight (which just contains all wavelengths with approximately the same spectral brightness) falls on the achromatic axis of the color space.
What every girl knows
Important consequences of the fact that a person’s color perception is three-dimensional and the spectral world is infinite-dimensional are metamerism radiation and metamerism stains.
Consider two different white lights – daylight and fluorescent. Unlike daylight, the power of luminescent light is not distributed throughout the spectrum, but is concentrated in several narrow sections. However, these areas are selected so that the responses of the “blue”, “red” and “green” cones are equal to each other, that is, so that the observer perceives the light as white.
Thus, we see that both there and there, the observer fixes a white color, although the initial spectra have nothing to do with this – this is called metamerism. It is the concept of metamerism that is hidden in Schroдингdinger’s definition: fixing the sensor, we factor the spectrum space in such a way that some spectra begin to be characterized by the same sensor reaction (and, accordingly, we say that they have the same color), and some – different (we say that their color is different). Nevertheless, it is possible to distinguish “two white lights” – passing the luminescent light through a prism, we will see a “torn” rainbow.
Miracles do not end there. There may be two colors (necessarily with different spectral characteristics), which, reflecting daylight, will lead to the same sensor response, and reflecting luminescent to different. Or vice versa. That is, for the same colors, metamerism will occur in one light, but not in another. And in this there is no psychology, only mathematics. And we are talking about quite life situations. Probably every girl knows that it is not worthwhile to pick up a skirt and blouse bought separately under fluorescent lighting, in the hope that they will fit each other in natural, although she does not know why.
All this is already slightly confusing, but we have not yet reached the worst.
So what is color?
The main confusion is what we call color three different things.
First, we call color sensation coloring. When we look for a shirt in a dark closet, we say “I see a red shirt” and not “I see a black shirt”, although, in fact, the radiation reflected from the shirt in the dark is so weak that it looks more like black. Red color in this case is a characteristic of the dye applied to the shirt fabric. Mathematically, color can be specified as a spectral characteristic – a function of reflectivity depending on the wavelength.
Secondly, color can be called a sensation. illuminationcreated by a light source. For example, we distinguish when a person has a green complexion, and when a green light just falls on his face. Illumination is determined by the spectral function of the radiation intensity depending on the wavelength.
And thirdly, there is color in the colorimetric meaning, that is, a feeling of the radiation that “flew” into our eyes. Since we always observe reflected light, this is the radiation of a light source reflected from the observed object and at the same time changed. According to the laws of physics, its spectral function is the product of the spectral functions of illumination and color:
Where – spectral function of the radiation entering the eye, Is the spectral function of the light source, Phi left ( lambda right) is the spectral characteristic of the color of the object.
Color consistency
In humans, the mechanism is known color consistency – the ability of the visual system to evaluate color under different lighting conditions. This is an evolutionarily important skill: for example, a monkey needs to know if the fruit has turned red or is it that the sunset light has fallen on him. To solve this problem, the human visual system, receiving even different signals from the sensors, can nevertheless find the two colors the same, but differently illuminated. This is a higher order phenomenon than metamerism. It belongs to the field of higher nervous activity and is still not sufficiently studied.
As we said, we can assume that from each point of the field of view 3 numbers enter the brain – the reactions of the “blue”, “red” and “green” cone receptors. Their values are specified as an integral over the wavelength:
Where – sensor response vector , – the vector function of the sensitivity of the “cones” of three types.
The calculation of such an integral occurs physically when light is reflected from an object, and then electrochemically when light provokes a response from the retina receptors, as a result of which three numbers characterizing color are formed.
To determine the color of an object, the human visual system solves the inverse problem: for each image point, from these three numbers and, possibly, known to the system of eigen characteristics, information is extracted on the spectral distributions of reflectivity and brightness of illumination.
These two functions come under the integral as a product, so the task of determining them looks like a mockery. Nevertheless, it can be argued that color consistency in a person works. The development of color constancy algorithms for technical vision is an urgent scientific task.
Where to apply this knowledge?
At Smart Engines, we have serious expertise not only in document recognition and authentication. We constantly participate in custom projects on various topics. computer vision. So, the color theory described in the article was applied in the X-ray region in order to sort diamond ore in Yakutia. The radiation passing through the rock was recorded by two detectors sensitive to different wavelength ranges. It turned out that all diamonds have the same color, different from the color of empty ore. Such “staining” made it easy to identify diamonds indistinguishable from ore in other ways.
The article was prepared on the basis of the materials of a public lecture by Dmitry Nikolaev, Ph.D., Technical Director of Smart Engines Service LLC, edited by Ph.D. Sergey Gladilin.




