Collatz Conjecture Part 1


annotation

This is the first article in the “Proof of the Collatz Conjecture” series, and to date the only article (in the world) that reveals the true nature of the Collatz Conjecture.
In this article, the author analyzes in detail the algorithm of the Collatz hypothesis, its structure, properties and features.

Keywords: Collatz conjecture, algorithm, recursion, recursion step, recursive descent, recursive ascent.

§ 1. Statement of the question

The Collatz conjecture is one of the unsolved problems in mathematics. Received wide popularity thanks to simplicity of a formulation.

Take any natural number n; If it is even, divide it by 2, and if it is odd, then multiply by 3 and add 1 (we get 3n+1); We perform the same operations on the resulting number, and so on.

What would be the starting number n we don’t take, sooner or later we will get a unit, the hypothesis says. And you have to prove it.

§2. Introduction

Legends about the unprovability of this problem have long been circulating in mathematical circles. For example, the American mathematician J. Lagarias recalls:
“In 1960, for more than a month, the entire Yale University worked on the problem 3n + 1 to no avail. It was something incredible. The same fate befell the researchers at the University of Chicago when I told them about this problem. There was a joke that 3n + 1 – this is a conspiracy of Soviet scientists against the United States to reduce America’s scientific potential and slow down our research in other areas.”

In 2007, mathematicians S. Kurtz and J. Simon came to the conclusion that the 3n+1 problem is not provable in this formulation of the question.
In 2010, the American Mathematical Society published the “Boundless Challenge for Mathematics: 3x+1” collection. This book is about unsuccessful attempts to find a solution for 3n+1.

Despite all this, the author, Mikhail Martynov, found strength in himself and revealed the true essence of the Collatz hypothesis. Therefore, this article is (to date) a breakthrough in the field of study 3n+1 and shows that the Collatz conjecture is just part of the algorithm. To prove the Collatz conjecture, we need to move on to a completely different problem.

§3. Full version of the algorithm

The hypothesis performs the actions 3n+1 and n / 2, then the reverse actions are: \frac {n–1}{3} And n*2.
We formulate it this way: Take any natural number n; If it is odd, then we multiply by 2. If it is even, then we subtract one from it (n–1); If the result of division \frac {n–1}{3} will be an integer, then it will be the next number; If not, then multiply n on 2; In general, we always multiply n by 2 to generate more and more new branches.

Let’s look at the sequences according to this scheme:

1, 2, 4, 1
1, 2, 4, 8, 16, 5
1, 2, 4, 8, 16, 5, 10, 3
1, 2, 4, 8, 16, 5, 10, 20, 40, 13
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11, 22, 7
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11, 22, 7, 14, 28, 9
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11, 22, 44, 88, 29, 58, 19

Note that these are the usual Collatz sequences, only they are reversed. Let’s write all this in more detail.

Let’s perform the transformation for 1:
Number 1. Multiply by 2. We get 2.

Let’s perform the transformation for 2:
Number 2. Multiply by 2. We get 4.

Let’s do the transformation for 4:
Number 4. \frac {4–1}{3} = 1
Number 4. Multiply by 2. We get 8.

Let’s perform the transformation for 8:
Number 8. Multiply by 2. We get 16.

Let’s do the transformation for 16:
Number 16. \frac {16–1}{3} = 5
Number 16. Multiply by 2. We get 32.

So, we are on the threshold of the first fork! 1, 2, 4, 8, 16 – here we have a fork at 5 and 32.

Let’s go to fork 5:
1, 2, 4, 8, 16, 5, 10 – here we again have a fork at 3 and 20.
1, 2, 4, 8, 16, 5, 10, 3, …
1, 2, 4, 8, 16, 5, 10, 20, …

Let’s go back to number 32:
1, 2, 4, 8, 16, 32, 64 – here we again have a fork at 21 and 128.
1, 2, 4, 8, 16, 32, 64, 21, …
1, 2, 4, 8, 16, 32, 64, 128, …

Let’s stop there.
The algorithm we just described is recursion. Algorithm 3n+1 reproduces actions \frac {n–1}{3}, but only in reverse order. Thus, 3n+1 is the reversed recursion from the recursion \frac {n–1}{3}. This is precisely the reason for the fact that 3n+1repeating mirror actions \frac {n–1}{3}descends to unity.

In other words, recursion \frac {n–1}{3} created a tree of numbers for us. recursion 3n+1 does not yet know what kind of tree it is, but walking on it is doomed to go down to 1:

§4. First conclusions

  • Firstly, this kind of recursion in mathematics is called backward recursion or runtime recursion (see the book by S. Kleene, Introduction to Metamathematics, [гл. IX, §46]).

  • Secondly, as is obvious, the recursion starts from 1. The unit is the progenitor of all branches.

  • Thirdly, the descent to one for each number occurs along its own unique branch.

  • Fourth, the unit cannot have any other progenitor than itself, because \frac {n–1}{3} And 3n+1 give for unit – unit (cycle 1, 4, 2, 1).

  • Fifth, the Collatz conjecture is an algorithm derived from the algorithm \frac {n–1}{3}and therefore preserving all its properties.

§5. Even numbers

Recursion step \frac {n–1}{3} seems incredibly complicated to us because of the presence of even numbers. But do they affect recursion?
Let’s look at the recursion step:

1
12
1, 2, 4
1, 2, 4, 1
1, 2, 4, 8, 16
1, 2, 4, 8, 16, 5
1, 2, 4, 8, 16, 32
1, 2, 4, 8, 16, 5, 10
1, 2, 4, 8, 16, 5, 10, 3
1, 2, 4, 8, 16, 5, 10, 20, 40
1, 2, 4, 8, 16, 5, 10, 20, 40, 13
…

We apply infinite multiplication by 2, and continue each sequence:

One gets the impression that the even numbers act as links between the odd numbers, and the step itself is based only on the odd ones.
Let’s check it out.

§6. Odd numbers

Let n is an odd number, then to move forward according to the rule \frac {n–1}{3}we have to:

Then for n ≡ 1 mod(3) we double the number of even numbers:

§7. tail recursion

Note that if we receive an odd number of the form n ≡ 0 mod(3) at any step, we will not be able to continue generating numbers \frac {2n–1}{3}or \frac {4n–1}{3}or \frac {8n–1}{3}or \frac {16n–1}{3}, or any other power of two 2^k.
Because if n ≡ 0 mod(3), then the solution to the equation (\frac {2^kn}{3} - \frac {1}{3}) comes down to: 2^kz - \frac {1}{3}. It does not have an integer solution.
Numbers of the form n ≡ 0 mod(3) will be called the tail of the recursion.

§8. special link()

Algorithm \frac {n–1}{3} implies constant multiplication by 2.
Whatever we do, we always multiply by 2. This is the answer to the question why all the odd numbers in the Collatz sequences are separated from each other by even ones.
In this case, a situation arises when an odd number can give us two branches of odd numbers at once (as in the figure above). Those. an odd number “splits” into two odd numbers.

First case

As we have already found out, if there is such an odd number n ≡ 2 mod(3), then it follows that there is also an odd number x = \frac {2n-1}{3}.
But if we multiply n by 8, then there will definitely be a number: y = \frac {8n–1}{3}. Because any number n ≡ 2 mod(3) can be represented as 3k–1then the equation y = \frac {8n–1}{3} comes down to the solution:

y = \frac{8(3k–1)–1}{3} = \frac{24k–9}{3}=8k–3which of course has an integer solution.

Is there a connection between the numbers obtained in this way: x And y?

x = \frac {2n–1}{3}, \; \; n = \frac {3x+1}{2}

y = \frac {8n–1}{3}, \; \; n = \frac {3y+1}{8}

\frac {3x+1}{2} = \frac {3y+1}{8}

y=4x+1

Yes, there is a connection.
In other words, from an odd number n ≡ 2 mod(3) we can get two numbers at once, the number x = \frac {2n-1}{3} and number y=4x+1.

Second case

As we have already found out, if there is such an odd number n ≡ 1 mod(3), then it follows that there is also an odd number x = \frac {4n–1}{3}.
But if we multiply n by 16, then there will definitely be a number: y = \frac {16n-1}{3}. Because any number n ≡ 1 mod(3) can be represented as 3k–2then the equation y = \frac {16n-1}{3} comes down to the solution:

y = \frac{16(3k–2)–1}{3} = \frac{48k–33}{3}=16k–11which of course has an integer solution.

Is there a connection between the numbers obtained in this way: x And y?

x = \frac {4n–1}{3}, \; \; \; n = \frac {3x+1}{4}

y = \frac {16n-1}{3}, \; \; n = \frac {3y+1}{16}

\frac {3x+1}{4} = \frac {3y+1}{16}

y=4x+1

Yes, there is a connection.
In other words, from an odd number n ≡ 1 mod(3) we can get two numbers at once, the number x = \frac {4n–1}{3} and number y=4x+1.

Thus, we set the recursion step between all odd numbers:

\frac{2n–1}{3} for the case n ≡ 2 mod(3),

\frac{4n–1}{3} for the case n ≡ 1 mod(3),

n=n for the case n ≡ 0 mod(3),
and constant application to already obtained numbers 4x+1.

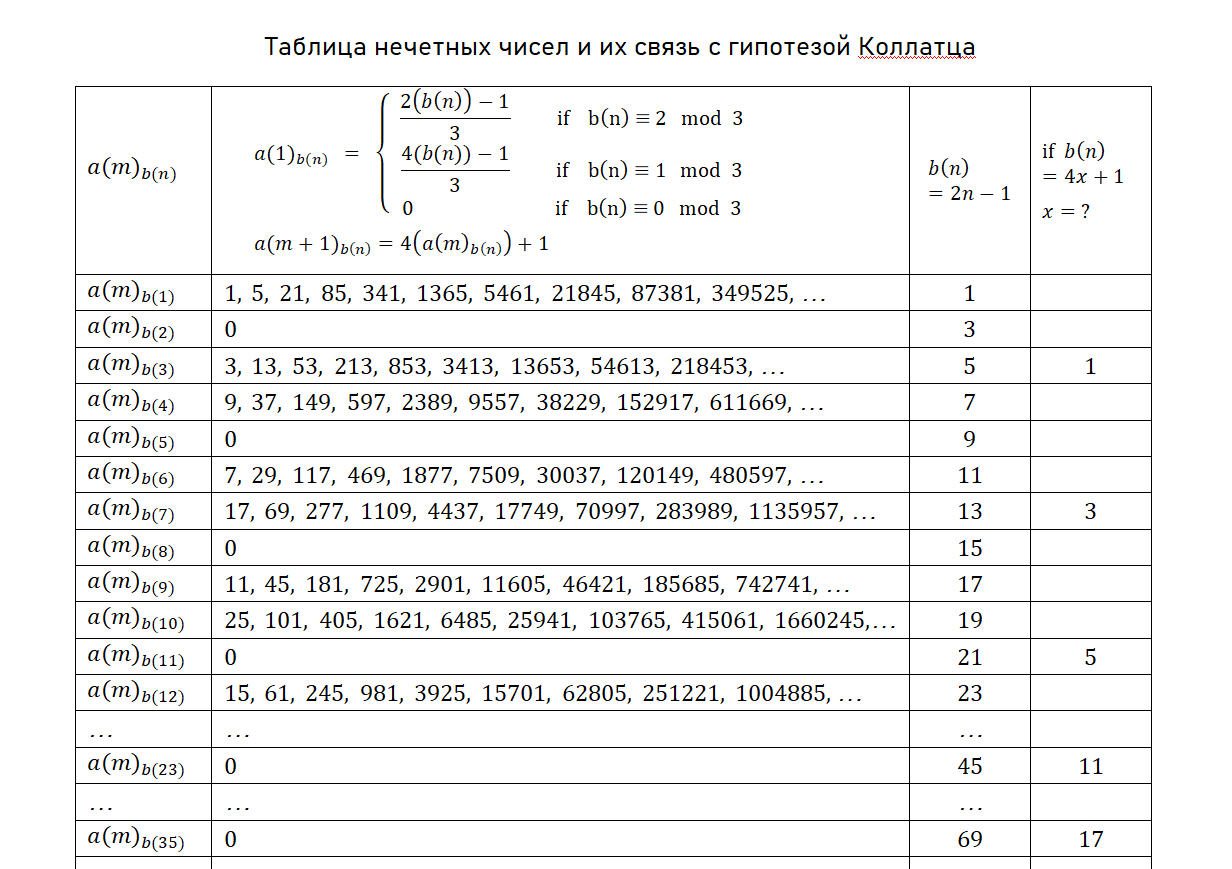
§9. New algorithm

We removed all even numbers from the recursion, and simplified the algorithm to apply only three rules \frac{2n–1}{3}, \frac{4n–1}{3} And 4x+1. Let’s write all this in more detail.

Iteration #1.
Number 1. n ≡ 1 mod(3), apply \frac{4n–1}{3}, \quad \frac {4–1}{3} = 1.
Number 1. 4n+1 = 5.

Iteration #2.
Number 5. n ≡ 2 mod(3), apply \frac{2n–1}{3}, \quad \frac {10–1}{3} = 3.
Number 5. 4n+1 = 21.

Iteration #3.
Number 3. n ≡ 0 mod(3), recursion tail.
Number 3. 4n+1 = 13.

Iteration #4.
Number 13. n ≡ 1 mod(3), apply \frac{4n–1}{3}, \quad \frac {52–1}{3} = 17.
Number 13. 4n+1 = 53.

Iteration #5.
Number 17. n ≡ 2 mod(3), apply \frac{2n–1}{3}, \quad \frac {34–1}{3} = 11.
Number 17. 4n+1 = 69.

Iteration #6.
Number 11. n ≡ 2 mod(3), apply \frac{2n–1}{3}, \quad \frac {22–1}{3} = 7.
Number 11. 4n+1 = 45.

Iteration #7.
Number 7. n ≡ 1 mod(3), apply \frac{4n–1}{3}, \quad \frac {28–1}{3} = 9.
Number 7. 4n+1 = 29.

etc.

§10. How to get the number 27?

In terms of recursion \frac {n–1}{3} it doesn’t matter which number is associated with which.
From the point of view of people, they like to invent anomalies.

In order to get the number 27, we just need to run a recursion from one and walk along the following branch:

1 \rightarrow 5 \rightarrow 3 \rightarrow 13 \rightarrow 53 \rightarrow 35 \rightarrow 23 \rightarrow 15 \rightarrow 61 \rightarrow 81 \rightarrow 325 \rightarrow 433 \rightarrow 577 \rightarrow 769 \rightarrow 3077 \rightarrow 2051 \rightarrow 1367 \rightarrow 911 \rightarrow 607 \rightarrow 2429 \rightarrow 1619 \rightarrow 1079 \rightarrow 719 \rightarrow 479 \rightarrow 319 \rightarrow 425 \rightarrow 283 \rightarrow 377 \rightarrow 251 \rightarrow 167 \rightarrow 111 \rightarrow 445 \rightarrow 593 \rightarrow 395 \rightarrow 263 \rightarrow 175 \rightarrow 233 \rightarrow 155 \rightarrow 103 \rightarrow 137 \rightarrow 91 \rightarrow 121 \rightarrow 161 \rightarrow 107 \rightarrow 71 \rightarrow 47 \rightarrow 31 \rightarrow 41 \rightarrow 27.

§eleven. Implementing recursion on a computer

Recursion is the simplest, in terms of implementation. To generate new numbers, you need to recursively execute the following piece of code, starting from one:

Процедура ПрименитьПравила(n)
    
	Если (n % 3 = 1) Тогда
		ПервоеЧисло = (4*n - 1)/3;
		ВтороеЧисло = 4*n + 1;
	КонецЕсли;
	
	Если (n % 3 = 2) Тогда
		ПервоеЧисло = (2*n - 1)/3;
		ВтороеЧисло = 4*n + 1;
	КонецЕсли;

	Если (n % 3 = 0) Тогда
		ПервоеЧисло = 0; // хвост рекурсии
		ВтороеЧисло = 4*n + 1;
	КонецЕсли;
	
	ДобавитьНовоеЗначениеВТаблицу(ПервоеЧисло);
	ДобавитьНовоеЗначениеВТаблицу(ВтороеЧисло);
	
КонецПроцедуры

To cover the interval from [1 … 100] 500 iterations are required.
To cover the interval from [1 … 1000] 25,000 iterations are required.
To cover the interval from [1 … 10000] 1 million iterations are required.

Sincerely,
Article author: Mikhail Martynov

Similar Posts

Leave a Reply

Your email address will not be published. Required fields are marked *